こちらでは、pH(水素イオン指数)へと導くために、不可欠な常用対数の基礎について記載してあります。更に、常用対数に関連のある指数等を交えながら、基礎的pHを理解していきましょう。
また、pH計算に必須となる、水のイオン積:Kw、pKw、水酸化物イオン指数:pOH等にも着目していきましょう。
皆さんがpH・pOHを求めるには、累乗根(=2乗根√)、指数等の他に、避けては通れない常用対数があります。
特に難しい常用対数を考える必要はなく、基本的な流れを理解してもらいますと充分対応出来ますので、1つ1つを確実にこなしていきましょう。
通常、pH・pOHは一般的な常用対数を、逆数の常用対数として扱っています。最初は少々戸惑われるかもしれませんが、やり方としては全く同じ様な求め方となっていますので御安心下さい。
さらに、常用対数は「❂ 累乗根」と併せて、またpHの基本も理解して頂きたいとも思いますので、
「前代未聞!?弱酸のpH&pOHを制覇する術(すべ)、此処に在り!」
「前代未聞!?弱塩基のpH&pOHを制覇する術、此処に在り!」
で紹介しています基本的な累乗根・pH&pOHの別記事も是非御覧下さい!
それでは今回、画像(私が記述しました)を基に話を進めていきますので、宜しくお願い致します。
それではスタートです!
1.「 常用対数 & pH(水素イオン指数)!」

ここでは、常用対数とpHが、どの様な仕組みによって表されているかを、最初で簡単に紹介していきます。これにより、皆さんが「pHという、おおよその全体像が観える!」と思われます。少々長くなりますが、バラバラではなく、一気にpHに必要な基礎的なものの流れとしてスムーズにまとめてありますので、ゆっくり時間を掛けて御理解下さい!

通常の常用対数は、上記の様に、「指数」と深い関係があります。この様に、常用対数を考える場合、簡単な数字を自分でlogの真数として入れ込んだ方が理解しやすいと思います。真数に少々厄介な分数とか記述してある場合にも、考え方自体は全く同じですので、まずはこの様な簡単な事から始めていきましょう。
では次に、pHについて考えてみましょう(※ 後程、常用対数につきましては、再度触れていきます)。
( 2.)pHは一般に、H^+(水素イオン)の濃度の逆数の常用対数として、0~14までの範囲で表されています。その範囲の中心:pH=7より小さい範囲(pH<7)を酸性、pH=7:中性、pH=7より大きい範囲(pH>7)を塩基性(アルカリ性)と呼んでいます。
イメージとしては、両手を真横に広げ、左端指先が水素イオン濃度:[H^+]がMAXで強酸の0、頭上が中性の7、右端指先が水酸化物イオン濃度:[OH^-]がMAXで強塩基の14、という様な感じです。
大まかですが、塩酸、硝酸、硫酸と呼ばれるpH=0~2程度の「強酸の水素イオンH^+を、水酸化物イオンOH^-で中和」していくと、中和される度に「※水H2Oが生じ」、pH=0の左方向から右方向へと移動し、pH=3~6程度の弱酸に、更に中心となるpH=7の中性に、そして中性を越えると、pH=8~12程度の弱塩基、最後はpH=13~14の強塩基の水酸化物イオン濃度:[OH^-]がMAXになります。
逆に、「強塩基の水溶液を、水素イオンH^+で中和していく」と、こちらも中和する度に水H2Oが生じ、全く真逆の現象が生じ、pHが左方向へと移動し始めます。最後はpH=0の、強酸の水素イオン濃度:[H^+]がMAXになる、といった様な大まかなイメージです。
H^+ + OH^- → H2O
[2]また、pH=7の中性付近では、水H2Oが僅かに電離(水溶液中で、ある物質が溶解し、陽イオン:H^+等と、陰イオン:OH^-等とに分離する現象)し、極僅かに右方向に進むと考えられますが、平衡は大きく左方向に偏り水H2Oへと戻ります(本来、水H2Oとして存在しているために、水H2O自体があまり電離せず、水H2Oに戻ろうと平衡が左方向に大きく偏ります!)。
H2O ⇔ H^+ + OH^-(※ 水H2Oが電離しても、☆平衡が大きく左に偏り、水H2Oに戻ろうとする。つまり、H^+とOH^-になりたくないという事です!)
純水の場合25℃で、水素イオン濃度:[H^+]と、水酸化物イオン濃度:[OH^-]の両イオンの濃度は共に、濃度:1.0×10^(-7)〔mol/L〕です。つまり、pH=pOH=7(※ pHと真逆的な性質を持つ、水酸化物イオン指数:pOHも存在します!)を示します。
またpH・pOHを求めるために必要である、[H^+]と[OH^-]の積によって表した値は、常に一定となる値である事から、水のイオン積と呼ばれ、記号:Kwと表します。「 ※ 水のイオン積:Kw=[H^+]×[OH^-]=H^+(mol/L)×OH^-(mol/L)=1.0×10^(-14)〔(mol/L)^2〕 」
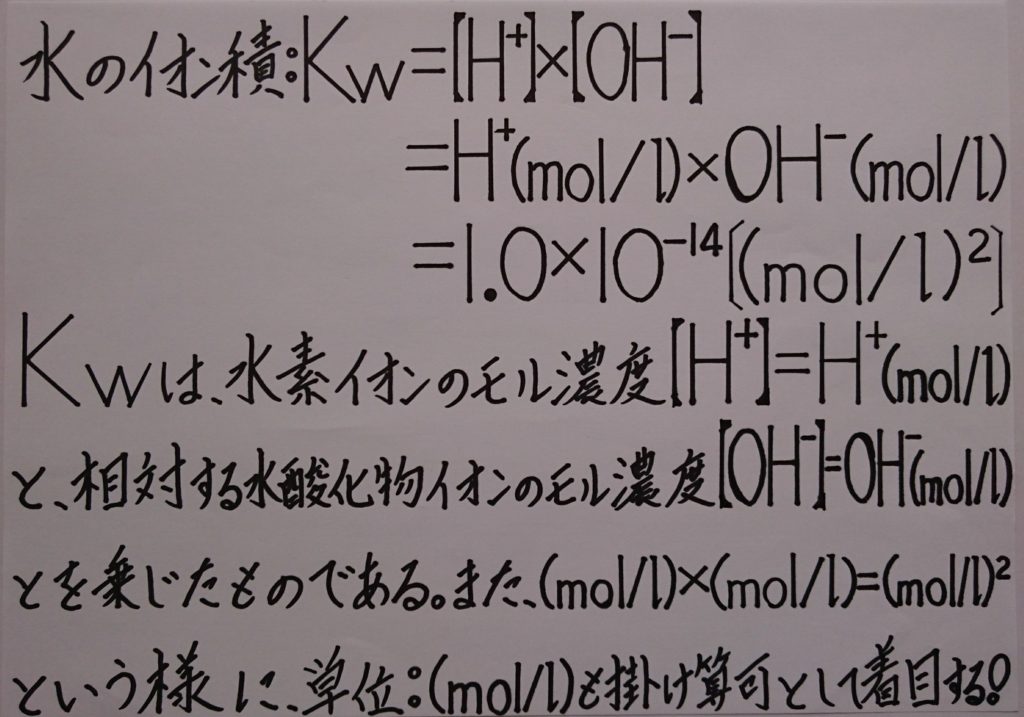
「※特に1.0の場合には、意味のない省略しがちの数字(後述してあります)!」でもあります。気付きにくい例として、「※ pKwの公式:pKw=-log(10)[Kw]の中にも存在し、次の様な立派な意味を所有しています!」
【※ pKw=-log(10)[Kw]=-log(10)[1.0×10^(-14)]=-(log(10)[1.0]+log(10)[10^(-14)])=-(0-14)=14 ∴pKw=14
つまりpKwの公式内の、log(10)[1.0]=0が、10を1.0にする指数は0、としての重要な意味を持ちます!】
この様に、常用対数に必要な存在ですので、省略せずにきちんと理解しておきましょう。
1-1.逆数の指数計算の確認をしておこう!
ここで、逆数同士の掛け算・割り算の確認をしておきましょう。通常の指数計算とやり方は全く同じ様なものですので、すぐ理解出来ると思います。それでは始めましょう(※ ここでも、通常のモル濃度〔mol/L〕を、(mol/L)として扱っていきますので御了承下さい!)。
〔例〕:[H^+]=1.0×10^(-1)(mol/L)、[OH^-]=1.0×10^(-13)(mol/L)、Kw=1.0×10^(-14)〔(mol/L)^2〕 とし、[H^+]×[OH^-]=Kw より、
「 1.0×10^(-1)(mol/L)×1.0×10^(-13)(mol/L)=1.0×10^(-1)+^(-13)〔(mol/L)^2〕=1.0×10^☆-(1+13)〔(mol/L)^2〕=1.0×10^(-14)〔(mol/L)^2〕 ∴Kw=1.0×10^(-14)〔(mol/L)^2〕 」と計算出来ます。
「※ ☆-(1+13)の様に、マイナス(-)によって括(くく)れるのがポイントです!& モル濃度単位:(mol/L)も、指数を持つ(mol/L)^1と考え、掛け算すると、(mol/L)^1×(mol/L)^1=(mol/L)^(1+1)=(mol/L)^2 と、単位は掛け算、単位の指数は足し算出来る事に着目しましょう!」
[2]逆数同士の割り算の場合、指数は引き算になります。
Kw/[OH^-]=[H^+] より、「[H^+]= 1.0×10^(-14)〔(mol/L)^2〕/1.0×10^(-13)(mol/L)=1.0×10^(-14)-^(-13)(mol/L)=1.0×10^☆-(14-13)(mol/L)=1.0×10^(-1) (mol/L) ∴[H^+]=1.0×10^(-1)(mol/L) 」と計算出来ます。
「※ ☆-(14-13)の様に、マイナス(-)によって括れるのがポイントです!& モル濃度単位:(mol/L)も、指数を持つ(mol/L)^1と考え、割り算すると、(mol/L)^2/(mol/L)^1=(mol/L)^(2-1)=(mol/L)^1=(mol/L) と、単位は割り算、単位の指数は引き算出来る事に着目しましょう!」また、
Kw/[H^+]=[OH^-] でもある事から、「[OH^-]= 1.0×10^(-14)〔(mol/L)^2〕/1.0×10^(-1)(mol/L)=1.0×10^(-14)-^(-1)(mol/L)=1.0×10^☆-(14-1)(mol/L)=1.0×10^(-13)(mol/L) ∴[OH^-]=1.0×10^(-13)(mol/L)」と計算出来ます。
(※☆-(14-1)の様に、マイナス(-)によって括れるのがポイントです!& 同じく、モル濃度単位:(mol/L)は、割り算出来ます!)
【※ 単位も、掛け算・割り算が出来、同時に、単位の指数は、足し算・引き算が出来ます!】
いかがでしょうか?☆のマイナス(-)によって括れる部分に着目し計算されますと、更に理解度が増すと思います!
[H^+]=1.0×10^(-7)(mol/L)と判明している場合、「 Kw=[H^+]×[OH^-]」に[H^+]を代入する(※[OH^-]を代入すると、pHが求められます!)と、
「 1.0×10^(-7)(mol/L) ×[OH^-]= 1.0×10^(-14)〔(mol/L)^2〕 」→ 「[OH^-]=1.0×10^(-14)〔(mol/L)^2〕/1.0×10^(-7)(mol/L) 」→ 「 1.0×10^(-14)-^(-7)(mol/L) 」 → 「 1.0×10^-(14-7)(mol/L) 」 → 「 1.0×10^(-7)(mol/L) 」 ∴ [OH^-](水酸化物イオン濃度)=1.0×10^(-7)(mol/L)
これより、pOH(水酸化物イオン指数)は、
「 pOH=-log(10)[OH^-]=-log(10)[1.0×10^(-7)] 」→ (logの真数の掛け算は、logの足し算で計算出来る事から) →「 -(log(10)[1.0]+log(10)[10^(-7)]) 」→ 「 log(10)[1.0]=0とし、log(10)[10^(-7)]の指数^(-7)はlogの前に出せる事から整理すると 」→ 「 -(0-7)=7 」 ∴ pOH=7
水のイオン積:Kwの他にも、Kwと似た公式があります。それが、前述したpKwを利用した公式「※ pH + pOH = 14(pKw) 」 であり、これに先程のpOH=7を代入すると、今度は、pHが求められます。
「 pH+pOH=14より、 pH+7=14 → pH=14-7 ∴ pH=7 」
といった様な繋がりがあります。 ※ 後程下方の画像を、御覧下さい!
※ 後程下方の画像を、御覧下さい!
1―2.「 pH(水素イオン指数)は、水素イオン濃度H^+〔mol/L〕の逆数の常用対数!」とは何ぞや!? & その仕組み!
[○]:10^(-2)=0.01(正:+)、[×]:10^(-2)=-2(負:-)」
パッと見ると、-(マイナス)であるかの様に勘違いしがちですが、正(+)であって、決して負(-)ではない事に注目しておきましょう!
ちなみに、当たり前に正としてインプットするために、「10^(-2)=0.01、10^(-5)=0.00001などに置き換えて考えると良いです。やり方として、指数の数だけ0を書いて、小数点(.)を打つだけで正として完成しますので、是非お試し下さい!」
〔注意!?〕「 [×]:2.0×10^(-3)=0.001、などは不正解です。2.0などの部分を、つい間違えやすいので気を付けましょう![○]:2.0×10^(-3)=0.002です!」
「(1):pH=- ↓ (2):log(10)[H^+]⇔(3):log(10)[100]=2 」
右「(2):log(10)[H^+]」を観ると、通常の常用対数である事が解ります。これに、最初の画像の常用対数:100(真数)を[H^+](真数)に代入すると、(2)と(3)の全く同じ常用対数である事が解ります。
そして、これに左「(1):pH=-」を加え、「(3):log(10)[100]=2」より、「答:2」を「(1):pH=-」の後に答として入れ込むと、「答:pH=-2」となってしまいますが、これは「不正解[×]:pH=-2」です!
【 何故なら、「 pH=pOH=0~14 」と、決して負(-)になる事はないからです。つまり、(3)の様な「※ 通常の常用対数では、pH・pOHは成立しない!」という事になります。そこで正として成立するために、真数部分に逆数を持ってくるのです!】
[3.]まず、(2)の通常の常用対数:log(10)[H^+]の[H^+](真数)に、例:[1.0×10^(-2)]を代入すると、「(2):log(10)[H^+]=log(10)[1.0×10^(-2)]」→ (ここで真数の掛け算:[1.0×10^(-2)]は、2つのlogを利用し、足し算によって求められますから、) → 「log(10)[1.0]+log(10)[10^(-2)]=0-2=-2」の負(-)の答が生じます。
[4.]後は、「(1):pH=-」の「-(マイナス)」に、上記の「答:-2」を乗じると、「(1):pH=(-)×(-2)=2 よって、答:pH=2」となり、pHが成立します!これをまとめると、
pH=-log(10)[H^+]=-log(10)[1.0×10^(-2)]=-(☆log(10)[1.0]+log(10)[10^(-2)])=-(0-2)=2 ∴ pH=2
【※ 特に上記[4.]式内の☆に注目します!ここで、[H^+]の逆数の常用対数の特徴として、( )内が、必ず負(-)の値になる様になっており、これが「-(0-2)」の( )内を指しています!( )内が、この負(-)になる事によって、最終的に求めるpHが正として成立するのです!】
皆さん、いかがでしょうか?これがpHの成立する仕組みとなっています。ですので、この( )内が負(-)になる様に計算する事を心がけておいてもらいますと、理解しやすくなると思いますので、是非お試し下さい。
【※ [H^+]の逆数の常用対数の確認につきましては、pH・pOHの基礎となるべき、
「前代未聞!?弱酸のpH&pOHを制覇する術(すべ)、此処に在り!」
「前代未聞!?弱塩基のpH&pOHを制覇する術、此処に在り!」
こちらを是非御覧下さい!】
[1.]pH=-log(10)[H^+]=-log(10)[2.0×10^(-5)]=★-log(10)[2.0]+5=4.7
[2.]pH=-log(10)[H^+]=-log(10)[2.0×10^(-5)]=「☆-(log(10)[2.0]+log(10)[10^(-5)])」=-(log(10)[2.0]-5)=★-log(10)[2.0]+5=-0.3+5=4.7
[2-1.]pH=-log(10)[H^+]=-log(10)[2.0×10^(-5)]=「☆-(log(10)[2.0]+log(10)[10^(-5)])」=-(0.3-5)=4.7
[1]と[2]を見比べると、「☆」の計算が省略してあるのが解ります。★の式が、だいぶ後ろの方へ来ています。この事から解ります様に、最初は出来るだけ[2]の式を意識して使った方が、式全体の流れが理解出来ると思います。式に慣れて来ましたら、[1]あるいは[2-1.]の省略された式へと、自然に移行されると良いと思います。まず、この形を完全に理解しましょう!】
(1.0×10^(-14))÷(1.0×10^(-14))=(1.0×10^(-14))/(1.0×10^(-14))=1.0×10^(-14)★-^(-14)=1.0×10^-(14-14)=1.0×☆10^(-0)=1.0×☆10^(0)=1.0×☆1=1
同じ数を同じ数で割ると、「答=1」なんですが、指数計算すると、結局計算式の中で、割り算、掛け算、引き算、足し算(※ ややこしいですが、★の部分です!)を全て使っちゃって、こんなに長くなるんですから、不思議と言えば不思議ですよね。
因(ちな)みに、「 ☆10^(-0)=10^(0)=1 」忘れがちですので、再度確認しておきましょう♪また、前画像の続きと致しまして、次の画像で、通常の常用対数と、逆数の常用対数との違いを大まかに記述しておきましたので、こちらの方も確認されたらと思います。似たような計算ですが、
「※ 1.0×10^(-14)÷1.0×10^(-14)=1.0×10^-(14+14)=1.0×10^(-28)!」は、割り算してから、最終的には掛け算によって、指数は足し算になりますので、お間違えのない様にして下さい!また、指数が負(-)でない場合の様な次の2つの計算につきましても、
「※ 1.0×10^(14)÷☆(1.0×10^(14))=1 」
「※ 1.0×10^(14)÷1.0×10^(14)=1.0×10^(14+14)=1.0×10^(28)!」
の様に、☆( )が付いているだけで答えが違ってきますので、上記同様お間違えのない様に御注意下さい!
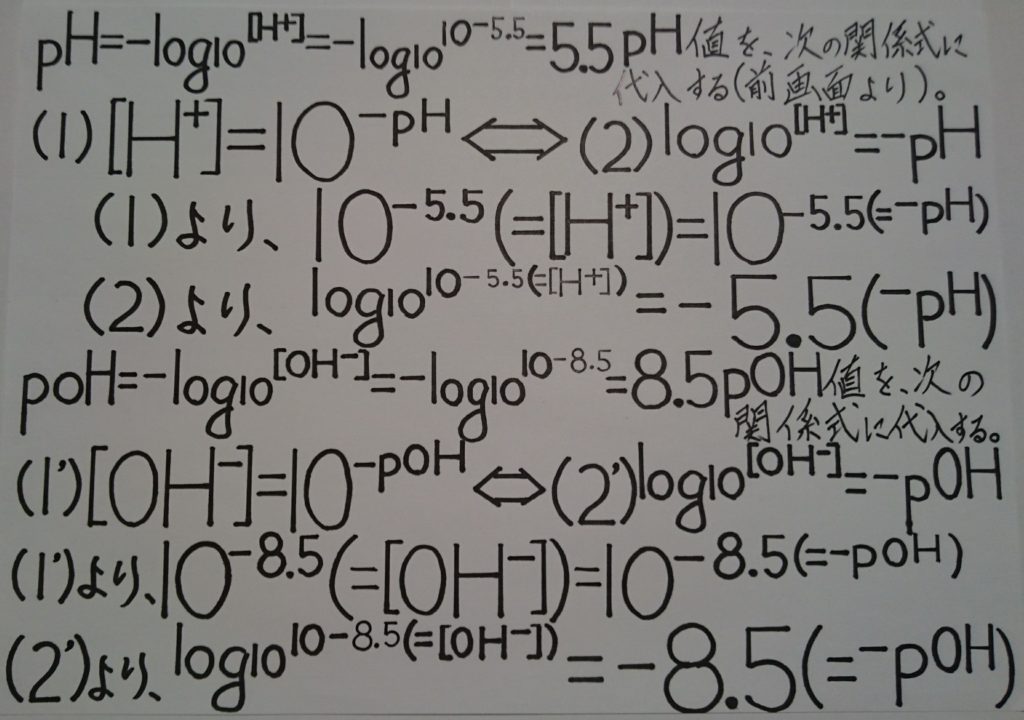
1-3.問題文の条件として登場する、常用対数の基礎を把握しよう!
最後に、pH・pOHの問題文の条件として使われる常用対数の基礎について理解しておきましょう。全て、10(底)とします。
問題文の条件として頻繁に出されるものに、「ただし、log(10)[2.0]=0.30、log(10)[3.0]=0.48とする。」という条件があります。これは、この条件を必ず使って下さいという事を指します(※ 中には必要な条件だけ使用し、不必要な条件は使用しなくても良い問題も存在する可能性がありますので、随時対応して下さればと思います!)。これら2つの常用対数は、真数が「1~10」の基礎的常用対数となっています。
そしてもちろん、pH・pOHにも大きな関連性がありますので、覚えるのではなく、意味を理解しながら、今一度再確認しておきましょう!
(3.)log(10)[3.0]≒0.48 ※ 以下これを使用します。
(4-1.)log(10)[4.0]=log(10)[2.0^2](=真数2.0^2の、指数2をlogの前に出せるため)=2log(10)[2.0](=2logの2は、指数を表し、log(10)[2.0]=0.30より)=2×0.30=0.60
[1]まず、log(10)[7.0]のままでは求めにくいので「7を2乗して、7^2=☆49」として考えます。更に「この☆49を間とした数値をとる!」という意味で、「48<☆49<50」として、これにより「☆49が、48と50との間の数値!」という事になります。
[2]「条件:log(10)[2.0]=0.30103、log(10)[3.0]=0.47712、をクリアする!」ために「48<49<50を、それぞれ(1/2)乗」します。
[3]「 48^(1/2)=√48=√(4^2×3)=√4^2×√3=4×√3=4√3 」⇔ 「 49^(1/2)=√49=√7^2=7 」⇔「 50^(1/2)=√50=√(5^2×2)=5×√2=5√2 」⇒ これより「 4√3<7<5√2 」として、計算していきます!
[4](48<49<50)^(1/2)より、「 4√3<7<5√2 」とし、「※ これら全てをlogとして扱い、条件を当てはめていきます!」
[5]「 log(10)[4√3]=log(10)[2^2×3^(1/2)](=真数4√3は掛け算であり、√3=3^(1/2)より、2^2×3^(1/2) と出来る)=log(10)[2^2]+log(10)[3^(1/2)](=真数の掛け算は、logの足し算に出来る)=2log(10)[2.0]+(1/2)log(10)[3.0](=真数2^2と、3^(1/2)の指数を、logの前に出して計算すると)=2×0.30103+(1/2)×0.47712=0.84062 」
[6]「 log(10)[5√2]=log(10)[5×2^(1/2)](=真数5√2は掛け算であり、5=(10/2)の分数に、√2=2^(1/2)と出来る)=log(10)[(10/2)×2^(1/2)](=真数(10/2)は、logの引き算に、掛け算はlogの足し算に出来る)=(log(10)[10.0]-log(10)[2.0])+(1/2)log(10)[2.0](=log(10)[2.0]=0.30103を代入すると)=(1-0.30103)+(1/2)×0.30103(=log(10)[10.0]=1、とし計算すると)=0.849485
[7]:[5]と[6]より、「 0.84062<log(10)[7.0]<0.849485 」
[8]∴ log(10)[7.0]≒0.84(=log(10)[7.0]=0.8451より) 】
(8-1.)log(10)[8.0]=log(10)[2.0^3](=真数2.0^3の、指数3をlogの前に出せるため)=3log(10)[2.0](=3logの3は、指数を表し、log(10)[2.0]=0.30より)=3×0.30=0.90
(9-1.)log(10)[9.0]=log(10)[3.0^2](=真数3.0^2の指数2は、logの前に出せるため)=2log(10)[3.0](=2logの2は、指数2を表し、log(10)[3.0]=0.48より)=2×0.48=0.96
皆さん、これらの常用対数は、基礎中の基礎ですので、流れを1つ1つ理解して頂いて、pH・pOHを制覇していきましょう!
最後に今回も含め、ここから先は何といっても「※ 化学に必要なイメージ力!」が非常に大事になって来ると思います。皆さん、目に観えるものと、目に観えないものの両方を相手にしていく訳ですので、自分なりのイメージを持つ事は、理解度を左右する程の重要さになっていくでしょう。
理解度が増して来ると、例えイメージが誤っていたとしても、すぐに修正が出来ますので、観えない相手には、自分なりのイメージ力をどんどん膨らませていきましょう!では、この辺でまた! See you !




















