「風が気持ち良か、もうすぐ春ぜよ!ストロング待ち遠しいぜよ!」
今回も「ぜよぜよ!」言ってみました。また、タイトルとは何の関係も無いセリフですので御了承下さい!
さて今回は、「強酸を希釈するとpHはどうなる?バージョン」より、
「塩酸HClを薄〜くするとpHはどう変化する?」
についてやってみたいと思います。
考え方は強塩基を希釈してpHを求めるやり方と何ら変わりませんので、皆さんスムーズに理解されるのではないでしょうか!
それでは、スタートです!
1.強酸を薄〜くするとpHはどうなる?

別記事でも記述しました様に、強酸を希釈すると強塩基同様に、pHを求める為の2つの解法が在ります。
ここでは再度、記述しておきます!
(1)強酸を希釈する場合において、水H2Oの電離を考慮しないpHの求め方。
「※ 希釈倍数した後の水素イオンH^+のモル濃度︰c〔mol/L〕」>「※ 希釈倍数して水溶液中に存在している、水素イオンH^+のモル濃度のおおよその基準︰10^-6〔mol/L〕」に基いて、希釈倍数し求めた水素イオン濃度H^+〔mol/L〕、あるいは水酸化物イオン濃度OH^-〔mol/L〕によって、pHまたはpOHを求める!
(2)強塩基を希釈する場合において、水H2Oの電離を考慮しないpHの求め方。
「※ 希釈倍数した後の水酸化物イオンOH^-のモル濃度︰c〔mol/L〕」>「※ 希釈倍数して水溶液中に存在している、水酸化物イオンOH^-のモル濃度のおおよその基準︰10^-6〔mol/L〕」に基いて、希釈倍数し求めた水素イオン濃度H^+〔mol/L〕、あるいは水酸化物イオン濃度OH^-〔mol/L〕によって、pHまたはpOHを求める
(1’)強酸を希釈する場合において、水H2Oの電離を考慮したpHの求め方。
「※ 希釈倍数した後の水素イオンH^+のモル濃度︰c〔mol/L〕」≦「※ 水H2Oの電離が、pHに影響を与える希釈倍数した水素イオンH^+のモル濃度のおおよその基準︰10^-6〔mol/L〕」に基いた、2通りの解の公式により求めた水素イオン濃度H^+〔mol/L〕によってpHまたはpOHを求める!
(2’)強塩基を希釈する場合において、水H2Oの電離を考慮したpHの求め方。
「※ 希釈倍数した後の水酸化物イオンOH^-のモル濃度︰c〔mol/L〕」≦「※ 水H2Oの電離が、pHに影響を与える希釈倍数した水酸化物イオンOH^-のモル濃度のおおよその基準︰10^-6〔mol/L〕」に基いた、2通りの解の公式により求めた水酸化物イオン濃度OH^-〔mol/L〕によって、pHまたはpOHを求める!
この様に、水H2Oの電離を考慮しない場合と、水H2Oの電離を考慮した場合による計算の判断基準は、水素イオン濃度H^+〔mol/L〕と水酸化物イオン濃度OH^-〔mol/L〕共に、
「✼ ≒(おおよそ)10^-6〔mol/L〕」
の基準となります!
繰り返しになりますが、この基準値はH2Oの電離を考慮する事によって、2次方程式から解の公式を導いて、pHまたはpOHを求める基準でもありますので、どうぞ御理解下さい!
2.強酸を希釈した場合のpHを解の公式で求めてみよう!︰(その1)
[✕]︰10^-5〔mol/L〕✕10^-3(倍)=10^-8〔mol/L〕=c〔mol/L〕
この様にpH8となり、結果pH7を飛び越えて塩基性を示す事になってしまいます。
【❋ 強酸又は強塩基をいくら希釈しても、pH7を飛び越える事はありません!】
「✪ ただし、HClを希釈したモル濃度はc〔mol/L〕ですから、後記述になりますが、これを解の公式に代入する事になります!」
この事から上記[2]の(1’)より、
「❉ H2Oの電離を考慮したpHの求め方!」
が必要となってきます。
そこで、HClを希釈したモル濃度︰c〔mol/L〕と、H2Oが電離した際に生じる水素イオン︰H^+と水酸化物イオン︰OH^-のモル濃度を利用して、水のイオン積︰Kwが成立する公式とします。
では、ここから順追って問題を解いていきましょう!
(1)︰まず、H2Oが電離した際に生じる水素イオン︰H^+と水酸化物イオン︰OH^-のモル濃度は互いに同じモル濃度である事に着目します!
H2O⇄H^+(電離したOH^-のモル濃度と全く同じ)+OH^-(電離したH^+のモル濃度と全く同じ)
生成した[H^+]と[OH^-]のモル濃度は全く同じである事から、これを未知数「x」とします。
[H^+](H2Oが電離したH^+)=[OH^-](H2Oが電離したOH^-)=x〔mol/L〕
(2)︰次に、(1)を利用してc〔mol/L〕を含んだ値として、水のイオン積︰Kwの公式に代入します!
総[H^+](✰ H2Oが電離したH^+〔mol/L〕+HCl希釈後のH^+〔mol/L〕=c〔mol/L〕)✕総[OH^-](✫ H2Oが電離したOH^-〔mol/L〕)=Kw
より、
[H^+]=x〔mol/L〕+c〔mol/L〕
[OH^-]=x〔mol/L〕
と考えて、水のイオン積︰Kwの公式に代入し2次方程式から解の公式を導くと、
(x+c)x=Kw
x^2+cx−Kw=0
x={−c★±√(c^2+4Kw)}/2
xの値は必ず0以上(x>0)である事から、分子の★−(マイナス)を外すと、
x={−c☆+√(c^2+4Kw)}/2
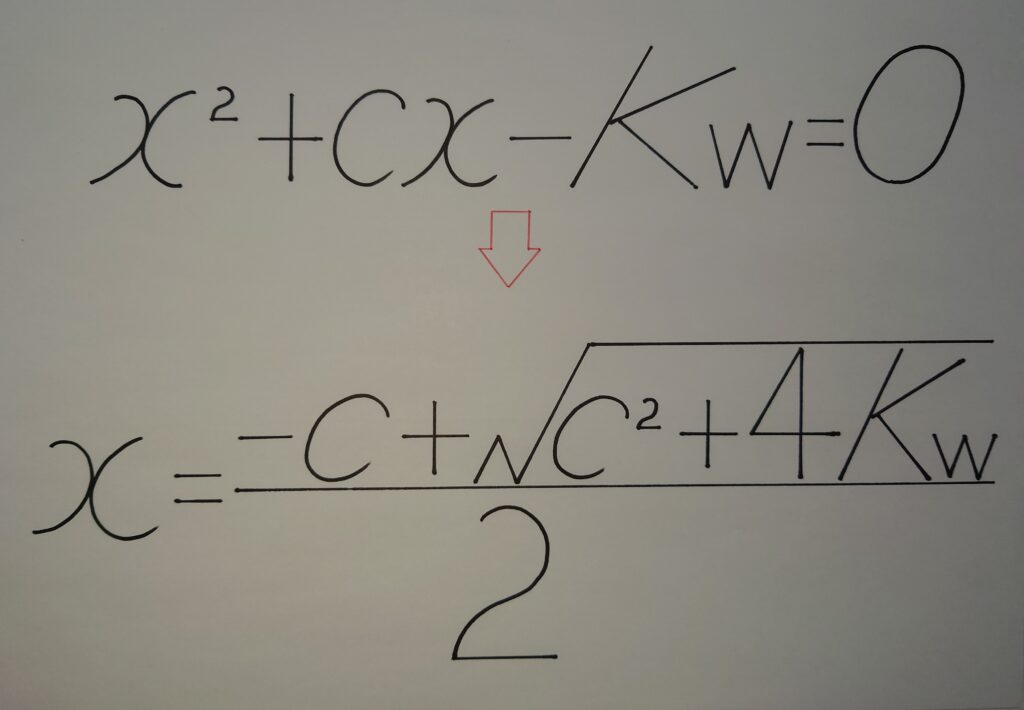
(3)︰cの値を求める為にHClを希釈倍数する!
10^-5〔mol/L〕✕10^-3(倍)=10^-8〔mol/L〕
(4)︰総[H^+]を求める為に、「解の公式により求めたx=H2Oが電離した[H^+]」と「HClを希釈倍数したcの値︰c〔mol/L〕」の和を計算式とする!
総[H^+]=x〔mol/L〕+c〔mol/L〕
より、
総[H^+]=c+x
=c+{−c☆+√(c^2+4Kw)}/2
={c☆+√(c^2+4Kw)}/2
(5)︰(4)の計算式にcの値︰10^-8〔mol/L〕とKwの値を代入する!
総[H^+]={c☆+√(c^2+4Kw)}/2
={10^-8+√{(10^-8)^2+4✕10^-14}}/2
={10^-8+√(10^-2+4)10^-14}/2
={10^-8+(10^-1+2)10^-7}/2
={10^-8+2.1✕10^-7}/2
ここで「10^-7」に合わせると、
={0.1✕10^-7+2.1✕10^-7}/2
=(0.1+2.1)10^-7/2
=(2.2✕10^-7)/2
=1.1✕10^-7
答.[H^+]=1.1✕10^-7〔mol/L〕
pH=−log(10)[H^+]
=−log(10)[1.1✕10^-7]
log(10)[1.1]=0.04 より、
=(0.04−7)
=6.96
答.pH=6.96
3.強酸を希釈した場合のpHを、解の公式で求めてみよう!︰(その2)
「2.」では「x」をH2Oが電離して生成した水素イオン濃度︰[H^+]として扱いましたが、ここでは、「全ての水素イオン濃度︰[H^+]」として水のイオン積︰Kwの式を成立させていきます。
(1)︰まず、HClをH2Oで希釈したモル濃度をc〔mol/L〕とします!
10^-5〔mol/L〕✕10^-3(倍)=10^-8〔mol/L〕=c〔mol/L〕
(2)︰総[H^+]をxとして水のイオン積︰Kwの式に代入します!
(✰x−c)✯x=Kw
左辺の「✰x」は総[H^+]を表しており、H2Oで希釈したHClのモル濃度︰c〔mol/L〕を差し引くと、H2Oが電離したH^+のモル濃度︰[H^+]が残ります。
ここで、このH2Oが電離した[H^+]は、同じくH2Oが電離した[OH^-]は全く同じモル濃度ですので、
(✰x−c)=「H2Oが電離した[OH^-]のモル濃度」
として考えます。
同じく左辺の「✯x」は総[H^+]として考えますと、次の様に水のイオン積︰Kwが成立する事になります!
(✰x−c)✯x=[OH^-]✕[H^+]=Kw
(3)︰(2)の式を完成させ2次方程式として解の公式を導きます!
(x−c)x=Kw
x^2−cx−Kw=0 より解の公式は、
x={c★±√(c^2+4Kw)}/2
必ずxは、x>0である事から解の公式の★±のマイナス(−)を消去すると、
総[H^+]=x={c☆+√(c^2+4Kw)}/2
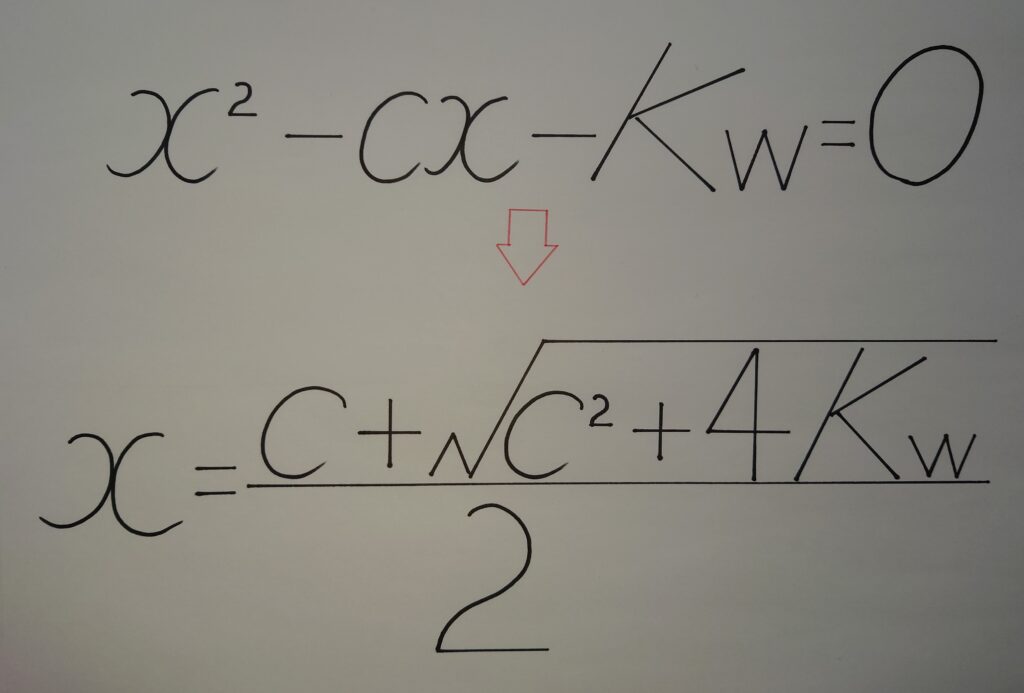
(4)︰HClをH2Oで希釈したモル濃度︰c〔mol/L〕が10^-8〔mol/L〕であるので、この値を解の公式に代入します!
総[H^+]=x={c☆+√(c^2+4Kw)}/2
x={10^-8+√{(10^-8)^2+4✕10^-14}}/2
={10^-8+√(10^-2+4)10^-14}/2
={10^-8+(10^-1+2)10^-7}/2
={10^-8+2.1✕10^-7}/2
ここで「10^-7」に合わせると、
={0.1✕10^-7+2.1✕10^-7}/2
=(0.1+2.1)10^-7/2
=(2.2✕10^-7)/2
=1.1✕10^-7
答.[H^+]=1.1✕10^-7〔mol/L〕
pOHはまずpHを求めます。
pH=−log(10)[H^+]
=−log(10)[1.1✕10^-7]
log(10)[1.1]=0.04 より、
=(0.04−7)
=6.96
pH+pOH=14 より、
pOH=14−6.96=7.04
答.pOH=7.04
【✺ 別解】「全ての水素イオン濃度︰[H^+]=HClをH2Oで希釈した後の水素イオン濃度︰[H^+]+H2Oが電離して生成した水素イオン濃度︰[H^+]」より、「H2Oの電離による水素イオン濃度︰[H^+]=x={−c+√(c^2+4Kw)}/2」 より、
x={−10^-8+√{(10^-8)^2+4✕10^-14}}/2
={−10^-8+√{(10^-16+4✕10^-14}}/2
={−10^-8+(10^-16+4✕10^-14)^(1/2)}/2
={−10^-8+(10^-8+2✕10^-7)^}/2
ここで、(10^-8+2✕10^-7)全体を「✰2✕10^-7」に合わせると、
={−10^-8+✰2✕10^-7(1+1/2✕10^-)^}/2
={−10^-8+✰2✕10^-7(1+0.05)}/2
10^-8を「−1.0✕10^-8」とし、全体を約分すると、
=(−0.5✕10^-8)+(1.05✕10^-7)
10^-7に合わせると、
=(0.05✕10^-7)+(1.05✕10^-7)
=(0.05+1.05)10^-7
=1.0✕10^-7〔mol/L〕
「全ての水素イオン濃度︰[H^+]=x(H2Oが電離して生成した水素イオン濃度︰[H^+])+1.0✕10^-8(HClをH2Oで1000倍希釈した後の水素イオン濃度︰[H^+])」より、
総[H^+]=x+1.0✕10^-8
x=1.0✕10^-7〔mol/L〕より、
=1.0✕10^-7+1.0✕10^-8
「10^-7」に合わせると、
=(1.0+0.1)10^-7
=1.1✕10^-7〔mol/L〕
答.[H^+]=1.1✕10^-7〔mol/L〕
pH=−log(10)[H^+]
=−log(10)[1.1✕10^-7]
log(10)[1.1]=0.04 より、
=(0.04−7)
=6.96
pH+pOH=14 より、
pOH=14−6.96=7.04
答.pOH=7.04
今回は、強酸を希釈した場合によるpHの求め方について言及してみました。やり方と致しましては、強塩基を希釈した場合と似たような解法である事が理解出来たのではないでしょうか?
また強塩基同様に上記問題は、2つ共に全く同じ内容の問題となっています。強酸の場合、強塩基の問題と比較すると理解しやすいのではないでしょうか!
解法と致しまして、強酸・強塩基をH2Oで希釈した場合のpHを細かい位まで求める為には、細かい値を求める過程で、どうしても2次方程式から解の公式へと導いてやる必要があります。
なので皆さん、この仕組みの意味を充分に理解された上で攻略しちゃって下さい!
それではこの辺で、また、 See you!



















