「太陽が眩しいぜよ!今年ん夏は暑うなるぜよ!」
タイトルを意識して、こんなん言うか分かりませんが、坂本龍馬風に「ぜよぜよ!」言ってみました!なお、タイトルの中身とは何の関係もないボヤキでした!
さて今回の本題は、
「強塩基を薄〜くするとpHはどうなる?」
についてです。
考え方と致しましては、
「強酸を薄〜くするとpHはどうなる?」
と、何ら変わらず同様に考えて頂けたらと思います。
それでは順番に進めていきましょう!
1.強塩基・強酸を薄〜くするとpHはどう変化する?

強塩基には水酸化ナトリウムNaOH、水酸化カリウムKOH、水酸化バリウムBa(OH)2、水酸化カルシウムca(OH)2等があり、これを希釈していくとpHは「2通りの状態!」を表します。
「❋ 1つ目は、希釈した倍数をモル濃度に乗じるだけでpHが求められる!」
「❋ 2つ目は、希釈した倍数をモル濃度に乗じるだけではpHを求める事が出来ない!」
の大きく2通りの状態に分けられます。
これは強酸である硝酸HNO3、塩酸HCl、硫酸H2SO4等も同様の考え方となります。
具体的例で、pHまたはpOHを求める問題文対策として文章化しますと、次の様にまとめられます。
(1)強塩基を希釈する場合において、水H2Oの電離を考慮しないpHの求め方。
「※ 希釈倍数した後の水酸化物イオンOH^-のモル濃度︰c〔mol/L〕」>「※ 希釈倍数して水溶液中に存在している、水酸化物イオンOH^-のモル濃度のおおよその基準︰10^-6〔mol/L〕」に基いて、希釈倍数し求めた水素イオン濃度H^+〔mol/L〕、あるいは水酸化物イオン濃度OH^-〔mol/L〕によって、pHまたはpOHを求める!
(2)強酸を希釈する場合において、水H2Oの電離を考慮しないpHの求め方。
「※ 希釈倍数した後の水素イオンH^+のモル濃度︰c〔mol/L〕」>「※ 希釈倍数して水溶液中に存在している、水素イオンH^+のモル濃度のおおよその基準︰10^-6〔mol/L〕」に基いて、希釈倍数し求めた水素イオン濃度H^+〔mol/L〕、あるいは水酸化物イオン濃度OH^-〔mol/L〕によって、pHまたはpOHを求める!
(1’)強塩基を希釈する場合において、水H2Oの電離を考慮したpHの求め方。
「※ 希釈倍数した後の水酸化物イオンOH^-のモル濃度︰c〔mol/L〕」≦「※ 水H2Oの電離が、pHに影響を与える希釈倍数した水酸化物イオンOH^-のモル濃度のおおよその基準︰10^-6〔mol/L〕」に基いた、2通りの解の公式により求めた水酸化物イオン濃度OH^-〔mol/L〕によって、pHまたはpOHを求める!
(2’)強酸を希釈する場合において、水H2Oの電離を考慮したpHの求め方。
「※ 希釈倍数した後の水素イオンH^+のモル濃度︰c〔mol/L〕」≦「※ 水H2Oの電離が、pHに影響を与える希釈倍数した水素イオンH^+のモル濃度のおおよその基準︰10^-6〔mol/L〕」に基いた、2通りの解の公式により求めた水素イオン濃度H^+〔mol/L〕によってpHまたはpOHを求める!
この様に、水H2Oの電離を考慮しない場合と、水H2Oの電離を考慮した場合による計算の判断基準は、水素イオン濃度H^+〔mol/L〕と水酸化物イオン濃度OH^-〔mol/L〕共に、
「✼ ≒(おおよそ)10^-6〔mol/L〕」
の基準となります!
2.強塩基を希釈した場合のpHを解の公式で求めてみよう︰(その1)
【❂ NaOHとH2Oの電離!】
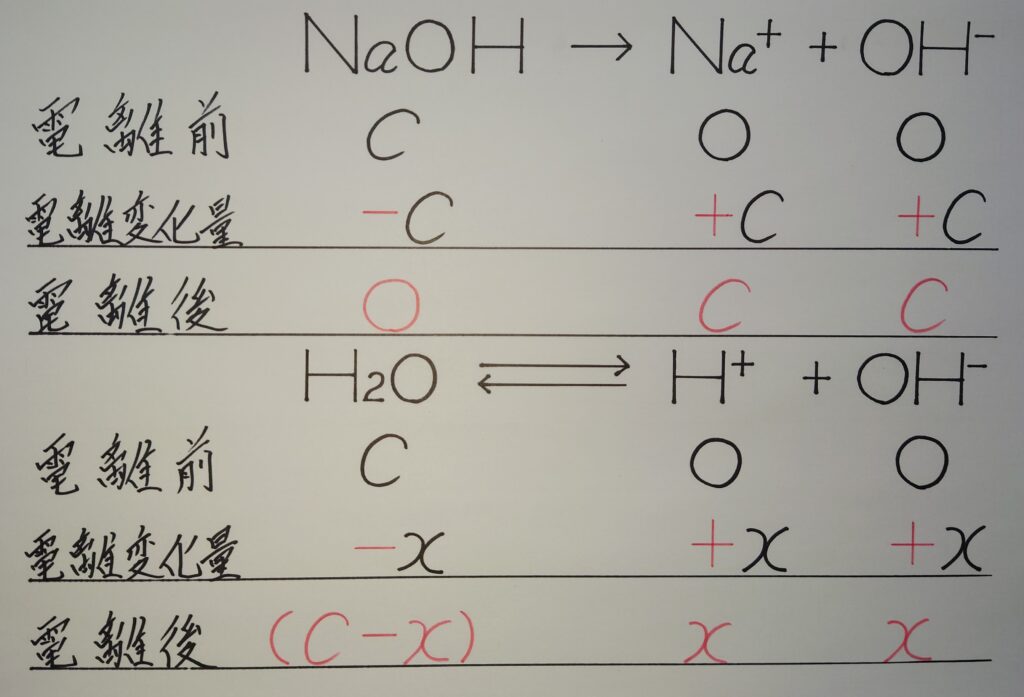
[✕]︰1.0✕10^-8〔mol/L〕✕10^-2(倍)=1.0✕10^-10〔mol/L〕
この様に計算してしまうと、pH10になってしまい、結局は弱塩基性を示すpOH4となります。
よって、強酸の様にpHを基準とするpH8を基準にして考えてしまいますと、pH10つまりpOH4になり強塩基を希釈した事にはならない結果となります。
そこで強塩基を希釈したpHを求める為には、水酸化ナトリウムNaOHが水溶液中で電離して塩基性を示している事から、まずは水酸化物イオン濃度︰OH^-〔mol/L〕を表している「pOH6︰1.0✕10^-6〔mol/L〕=✰c〔mol/L〕」の方を希釈倍数してみます!すると…
[✕]︰10^-6〔mol/L〕✕10^-2(倍)=10^-8〔mol/L〕=✰c〔mol/L〕
この様に水酸化物イオンOH^-のモル濃度が10^-8〔mol/L〕になり、pH7を超えてしまい酸性を表す事になってしまいます。結局、この計算方法でも希釈した場合のpHを求める事は出来ません!この事から次の様な事が言えます。
【❁ 強酸をいくら希釈してもpH7を超え塩基性になる事は決してない様に、強塩基をいくら希釈してもpH7を超えて酸性になる事は決してありません!】
『※ ただし、10^-8〔mol/L〕=✰c〔mol/L〕は、後記述の解の公式に代入する重要な値となります!』
この様にpH7を超えて酸性になるという事は、通常の計算ではpHを求められないという事になります。ここで考えられるのが、強酸を希釈した場合に必要とされる水H2Oの電離を、同じく強塩基にも利用するという考え方です。
H2O ⇄ H^+ + OH^-
このH2Oの電離が生じる基準は上記[2]の(1’)にある様に、水溶液中に存在する総水酸化物イオンOH^-のモル濃度が、おおよその基準︰≒10^-6〔mol/L〕として考えて頂けたらと思います。
この問題を解くには、H2Oが電離して生じるOH^-を、未知のモル濃度︰x〔mol/L〕として考え解いていく事が最重要となります。
H2O ⇄ H^+(=H2Oが電離したOH^-のモル濃度︰x〔mol/L〕と同じモル濃度である事から、計算式内では同じx〔mol/L〕として表す!) + OH^-(=x〔mol/L〕)
∴ 「❂ H2Oが電離したH^+とOH^-のモル濃度︰H^+〔mol/L〕=OH^-〔mol/L〕=x〔mol/L〕」
上記の様にH2Oが電離すると、H^+とOH^-のモル濃度は全く同じになります。よって、H^+もOH^-も「x」として計算式で使用されます。
「❋ これ等を基にして、以下の手順で水酸化物イオン濃度︰OH^-〔mol/L〕とpOHを求めていきます!」
(1)︰H2Oの電離を考慮し、電離した水酸化物イオンOH^-と、電離したH^+のモル濃度をx〔mol/L〕とする!
「OH^-〔mol/L〕=H^+〔mol/L〕=x〔mol/L〕」
(2)︰水酸化ナトリウムNaOHが完全電離して、これを希釈倍数し生成した水酸化物イオンOH^-のモル濃度をc〔mol/L〕とし、水のイオン積Kwを求める式に代入する!
OH^-〔mol/L〕=c〔mol/L〕 とし、
水のイオン積︰H^+〔mol/L〕✕OH^-〔mol/L〕=Kw〔mol/L〕^2 より、
x〔mol/L〕(x〔mol/L〕+c〔mol/L〕)=Kw〔mol/L〕^2
(3)︰(2)を2次方程式とする!
x(x+c)=Kw
x^2+cx=Kw
x^2+cx−Kw=0
「x(x+✰cα)=Kw」
[OH^-]=x>0(❁ [OH^-]の値は、必ず0より大きい!)より、分子の✰±の−(マイナス)は除外され次の解の公式となる!
【✺ H2Oが電離した[OH^-]=x={−c✰+√(c^2+4Kw)}/2】
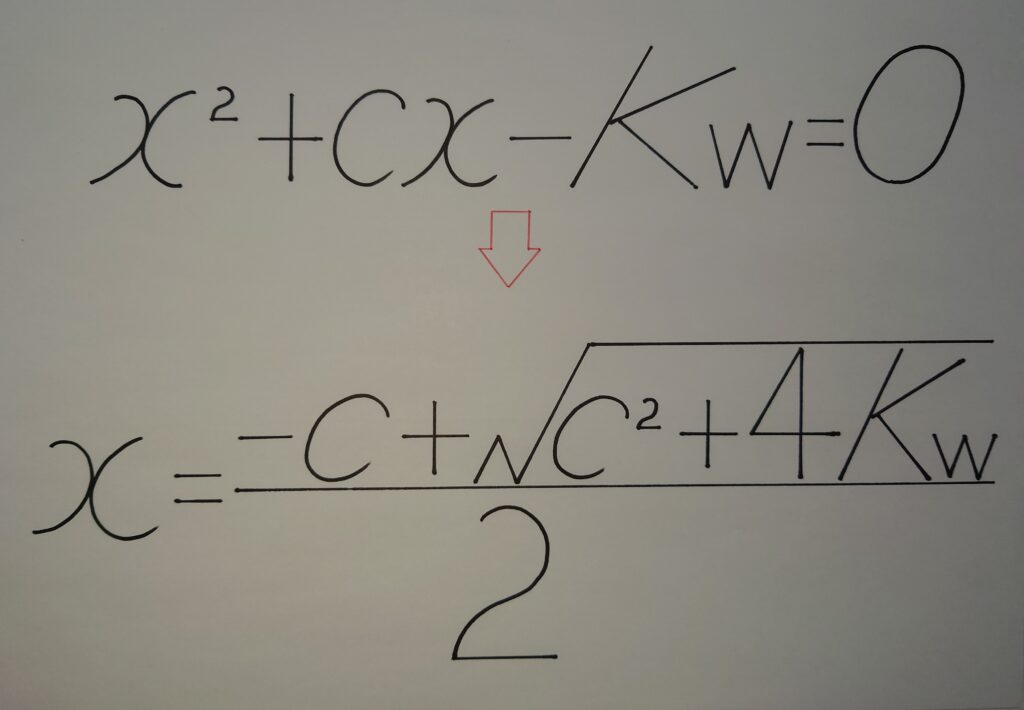
(6)︰ここで、pOHに必要な総水酸化物イオン濃度︰OH^-〔mol/L〕を求める計算式を作成する!
「x〔mol/L〕(H2Oが電離した[OH^-])+c〔mol/L〕(NaOHを希釈倍数した[OH^-])=総水酸化物イオン濃度︰[OH^-]」
x={−c✰+√(c^2+4Kw)}/2 より、
c+x=c+{−c✰+√(c^2+4Kw)}/2
=(2c/2)+{−c✰+√(c^2+4Kw)}/2
={c✰+√(c^2+4Kw)}/2
よって、
【✪ 総水酸化物イオン濃度︰[OH^-]={c✰+√(c^2+4Kw)}/2】
となり、この解の公式にそれぞれの値を代入し、総水酸化物イオン濃度︰[OH^-]を求める!
総水酸化物イオン濃度︰[OH^-]={10^-8+√{(10^-8)^2+4✕10^-14}}/2
={10^-8+√(10^-16+4✕10^-14)}/2
={10^-8+√(10^-2+4)✕10^-14}/2
={10^-8+√(0.01+4)✕10^-14}/2
={10^-8+√(4.01✕10^-14)}/2
={10^-8+√(4.01)✕10^-7}/2
ここで、「10^-8」を「1.0✕10^-8」とし、「√4.01≒2.0」とすると、
=(1.0✕10^-8)/2+(2✕10^-7)/2
=(0.5✕10^-8)+10^-7
ここで、「10^-8」に合わせると、
=(0.5✕10^-8)+(10✕10^-8)
これをまとめると、
=(0.5+10)✕10^-8
=10.5✕10^-8
答.[OH^-]=10.5✕10^-8〔mol/L〕
水酸化ナトリウムNaOHを希釈したpOHは、
pOH=−log(10)[OH^-]
=−log(10)[10.5✕10^-8]
log(10)[10.5]≒1.02 より、
=−(1.02−8)=6.98
答.pOH=6.98
因みにpHは、
pH+pOH=14より、
pH=14−6.98=7.02
∴ pH=7.02
3.強塩基を希釈した場合のpHを解の公式で求めてみよう!︰(その2)
ここでの考え方としましては、「2.」の問題と同様となります。
1.0✕10^-6〔mol/L〕の水酸化ナトリウムNaOHは、水酸化物イオン濃度︰OH^-〔mol/L〕を表している「pOH6=1.0✕10^-6〔mol/L〕」ですから、これを希釈倍数してみます!すると…
[✕]︰10^-6〔mol/L〕✕10^-2(倍)=10^-8〔mol/L〕
単純に希釈倍数してしまうと、モル濃度が10^-8〔mol/L〕になってしまい、pOH8となり酸性を示す事になり矛盾が生じてしまいます。
【❁ 強酸をいくら希釈してもpH7を超え塩基性になる事は決してない様に、強塩基をいくら希釈してもpH7を超えて酸性になる事は決してありません!
この考え方は、NaOHが存在している水酸化物イオンOH^-をいくら薄めても、水素イオンH^+に変化する事にはならないと言う単純なものです!】
よって、ここでも水酸化物イオンOH^-のモル濃度〔mol/L〕のおおよその基準が、
「10^-6〔mol/L〕>水酸化物イオン濃度︰OH^-〔mol/L〕」
の範囲にあれば、H2Oによる電離を考慮する必要があります。
さてpHの求め方ですが、「2.」と同様の2次方程式による解き方でも良いのですが、ここでは少々違う解き方で求めてみましょう。
「2.」と異なるのが、「x」の持つ意味です。「2.」では「x」を、H2Oが電離して生成するH^+とOH^-として考えましたが、ここでは「x」を、H2Oが電離して生成するOH^-と、水酸化ナトリウムNaOHが水溶液中で電離して生成したOH^-のモル濃度︰c〔mol/L〕とを、足した量として考えます。
【✺ x=H2Oが電離して生成するOH^-のモル濃度〔mol/L〕+水酸化ナトリウムNaOHが水溶液中で電離して生成するOH^-のモル濃度︰c〔mol/L〕】
つまり、
「x=[OH^-](H2Oの電離)+[OH^-](NaOH電離)=総OH^-〔mol/L〕」
という事になります。
「❋ そして、これ等を基にして以下の手順で「2.」と同様に、水のイオン積Kwを利用して総水酸化物イオン濃度︰OH^-〔mol/L〕を求めていきます!」
(1)︰H2Oの電離を考慮し、電離した水酸化物イオンOH^-と、電離したH^+のモル濃度をx〔mol/L〕とする!
「OH^-〔mol/L〕=H^+〔mol/L〕=x〔mol/L〕」
(2)︰水酸化ナトリウムNaOHが完全電離して、生成した水酸化物イオンOH^-のモル濃度をc〔mol/L〕とする!
OH^-〔mol/L〕=c〔mol/L〕
【x=H2Oが電離して生成したOH^-〔mol/L〕+NaOHが完全電離して生成したOH^-のモル濃度︰c〔mol/L〕】
の様に、「x」が「❋ 全ての水酸化物イオンOH^-濃度!」としての意味を持ちます!この「x」を水のイオン積Kwを求める式に代入します!
H^+〔mol/L〕✕OH^-〔mol/L〕=Kw〔mol/L〕^2 より、
(✰x〔mol/L〕−c〔mol/L〕)✯x〔mol/L〕=Kw〔mol/L〕^2
ここで理解しづらいのが、
(✰x〔mol/L〕−c〔mol/L〕)=水H2Oが電離し生成したOH^-〔mol/L〕
✯x〔mol/L〕=(H2Oが電離し生成したOH^-〔mol/L〕+水酸化ナトリウムNaOHが完全電離して生成したOH^-のモル濃度︰c〔mol/L〕)=総水酸化物イオン濃度OH^-〔mol/L〕
この様に考えますと通常、
[✕]︰OH^-〔mol/L〕✕OH^-〔mol/L〕=Kw
の様になってしまい、水のイオン積Kwが成立しません。
そこで、水のイオン積Kwを成立させるには、どうしても、いずれかのOH^-〔mol/L〕をH^+〔mol/L〕に置き換える必要があります。ここでは、()をH^+〔mol/L〕として置き換えられます。
(✰x〔mol/L〕−c〔mol/L〕)=H^+〔mol/L〕
何故置き換えられるのかと言いますと、
【(✰x〔mol/L〕−c〔mol/L〕)=H2Oが電離し生成したOH^-〔mol/L〕=H^+〔mol/L〕】
の様に、
(✰x〔mol/L〕−c〔mol/L〕)
の式から求められる値は、H2Oが電離して生成したOH^-とH^+の、どちらも同じモル濃度〔mol/L〕として求められますので置き換える事が可能なのです!これで、
(✰x〔mol/L〕−c〔mol/L〕)✯x〔mol/L〕=Kw〔mol/L〕^2
のイオン積Kwの式を、
(H2Oが電離して生成したH^+〔mol/L〕)✕{H2Oが電離して生成したOH^-〔mol/L〕+水酸化ナトリウムNaOHが完全電離して生成したOH^-のモル濃度︰c〔mol/L〕(=総水酸化物イオン濃度︰OH^-〔mol/L〕)}=Kw〔mol/L〕^2
として置き換える事が可能なのです。これより、
(x−c)x=Kw
の式が成立する訳です!
(x−c)x=Kw
x^2−cx=Kw
x^2−cx−Kw=0
(5)︰(4)の2次方程式を解の公式へと導く!
x^2−cx−Kw=0 より、xについて解くと、
x={c±√(c^2+4Kw)}/2
(5)︰「✪ 総水酸化物イオン濃度︰OH^-〔mol/L〕」=x={c✰±√(c^2+4Kw)}/2 より、
総OH^-〔mol/L〕=x>0(❁ 総OH^-の値は、必ず0より大きい!)より、解の公式の分子の✰±の−(マイナス)は除外され次の解の公式となる!
【✺ 総OH^-〔mol/L〕=x={c✰+√(c^2+4Kw)}/2】
【❆ 2次方程式より解の公式を導いて解く!】
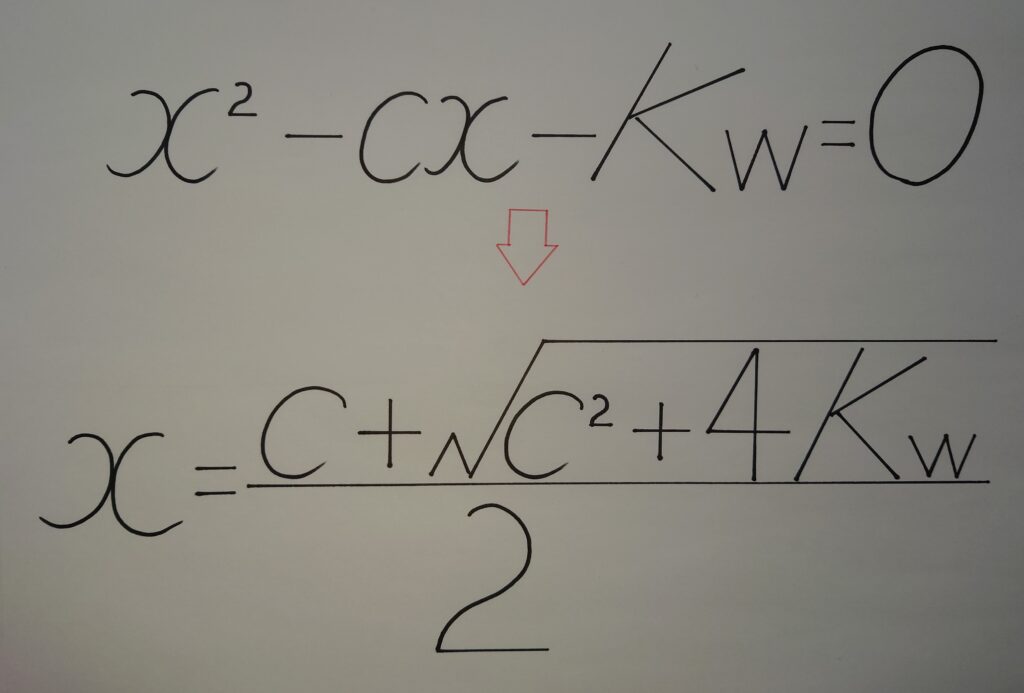
この解の公式に、それぞれの値を代入すると総OH^-〔mol/L〕が求められる!
総OH^-〔mol/L〕=x={c+√(c^2+4Kw)}/2
総OH^-〔mol/L〕=x={10^-8√{(10^-8)^2+4✕10^-14}}/2
={10^-8√(10^-16+4✕10^-14)}/2
={10^-8√{(10^-2+4)✕10^-14}}/2
={10^-8√{(0.01+4)✕10^-14}}/2
={10^-8√(4.01✕10^-14)}/2
={10^-8√(4.01)✕10^-7}/2
ここで「10^-8」を「1.0✕10^-8」にして計算し「√4.01≒2.0」とする!
=(1.0✕10^-8)/2+(2✕10^-7)/2
=✰(0.5✕10^-8)+10^-7
ここで「10^-8」に合わせると、
=(0.5✕10^-8)+(10✕10^-8)
=(0.5+10)10^-8
=10.5✕10^-8
答.[OH^-]=10.5✕10^-8〔mol/L〕
pHは直接求められないので、pOHをまず求めます!
pOH=−log(10)[OH^-]
=−log(10)[10.5✕10^-8]
log(10)[10.5]=1.02より、
=−(1.02−8)
=6.98
pHは、「pH+pOH=14」より、
14−6.98(=pOH)=7.02
答.pH=7.02
因みに、上記計算式「✰(0.5✕10^-8)+10^-7」を「10^-7」に合わせると、
総OH^-〔mol/L〕=x=(0.05✕10^-7)+(1.0✕10^-7)
=(0.05+1.0)10^-7
=1.05✕10^-7
ここでもpHは直接求められないので、pOHをまず求めます!
pOH=−log(10)[OH^-]
=−log(10)[1.05✕10^-7]
log(10)[1.05]=0.02より、
=−(0.02−7)
=6.98
pHは、「pH+pOH=14」より、
14−6.98(=pOH)=7.02
答.pH=7.02
結局、2問題共に最終的に扱う解の公式は、
{c+√(c^2+4Kw)}/2
という事になりますね!
今回は、強塩基を希釈した場合のpHとpOHを解の公式によって求めてみましたが、皆さんお気付きでしょうか?
上記の問題は、2問共全く同じ問題なのです。問題文の表現方法を少々変えただけなのですが、違った問題の様に感じます。
ここでは皆さんが応用化出来る様にと、2つの解の公式を使った問題を記述してみました。
重要な事として、強酸と強塩基を希釈した場合に解の公式を扱う関係性は、全く真逆の関係を表しているという事です!
つまり、総H^+〔mol/L〕と総OH^-〔mol/L〕の表し方が真逆の関係にあるのです!これについては、強酸を希釈した場合におけるpHの求め方についても御覧頂けたらと思います。
改めてpHって奥が深いですよね。だからこそ面白いんですよね!
それでは、この辺でまた、 See you!




















