こちらでは、2次方程式から、解の公式へと導く方法を、「別解」として紹介していきます。
前記事では、弱酸の電離度αを、2次方程式から解の公式へと導く事によって求められました。出来ましたら、前記事の、
で御理解された後、こちらを御覧頂きますと、更に理解度が増すと思われます。
さらに、pH、累乗根も関係性がある事から、
の別記事も是非御覧下さい!
今回、「別解」と称していますが、解法と致しましては、因数分解の公式を用いた、全く同じ様な解法となっていますので、ゆっくり時間を掛けて頂き御理解下さい。それでは、スタートです!
1.別解:解の公式への導き方!

「 cα^2+Kaα-Ka=0 」 →「(c/c)α^2+(Ka/c)α-(Ka/c)=0 」 →「α^2+(Ka/c)α-(Ka/c)=0 」(※ ここで、左辺:α^2+*(Ka/c)α に注目する!)
(2.) ※ 何故なら、解であるαを求めるためには、どうしても最終的な形として、因数分解の公式の右辺の、平方完成の形:「(x+a)^2 !」を、2次方程式の左辺に取り入れて、 「(α+Ka/2c)^2=(Ka^2+4cKa)/4c^2 」 とし、解を求めていく必要があるからだ!
(2.):因数分解の公式の左辺「x^2+2ax+a^2」 の形に変形する。ここで注目するのが、公式内の「x^2+2☆ax+★a^2」の☆★印の、「2☆ax」と「★a^2」である! まず、(1.):「*(Ka/c)α」を、(2.):因数分解の公式内の「2☆ax」と、全く同じ形にすると考えて、分数:(2/2)を乗じると、 「(Ka/c)α×(2/2)=2☆(Ka/2c)α」となり、「2☆(Ka/2c)α=2☆ax」となる。 これを、更に細かく分散すると、「α^2=x^2、係数2=係数2、☆(Ka/2c)=☆a 、項α=項x 」である事が理解出来る! 【α^2+係数2・☆( Ka/2c )・項α】 ⇔ 【 x^2+係数2・☆a・項x 】 同時に、「☆(Ka/2c)=☆a !」と言える事から、これを(2.):因数分解の公式「x^2+2☆ax+★a^2」内、「★a^2に代入」すると、 (1.):「α^2+*(Ka/c)α」は結局、次の(3.)式:「α^2+2☆(Ka/2c)α+★(Ka/2c)^2 」に、置き換えられる。 【※ (3.)式:α^2+2☆(Ka/2c)α+★(Ka/2c)^2 】 つまり、「α^2+*(Ka/c)α」は、因数分解の公式:x^2+2ax+a^2=(x+a)^2の左辺を利用し、「※一旦、α^2+2☆(Ka/2c)α+(Ka/2c)^2 に、置き換えられる!」 これより、「α^2+2☆(Ka/2c)α+★(Ka/2c)^2=x^2+2☆ax+★a^2=(x+☆a)^2!」の関係にあると言える! 更に、「α^2+2☆(Ka/2c)α+★(Ka/2c)^2=(x+☆a)^2 」 より、x=α、☆a=☆(Ka/2c) である事から、これを、因数分解の公式の右辺:(x+☆a)^2に代入すると、 ∴「α^2+2☆(Ka/2c)α+★(Ka/2c)^2=(α+☆Ka/2c)^2=(x+☆a)^2 」 として、平方完成となる! また、これを展開すると、 (α+☆Ka/2c)^2=(α+☆Ka/2c)(α+☆Ka/2c)=(3.)式:α^2+2☆(Ka/2c)α+★(Ka/2c)^2 であると確認出来る!
よって、これを差し引いた式が、最初の、(1.)式:「α^2+*(Ka/c)α」であり、「α^2+(Ka/c)α{=2(Ka/2c)α}」より、 (α+Ka/2c)^2-(Ka/2c)^2 =α^2+(Ka/c)α+(Ka/2c)^2-(Ka/2c)^2 =α^2+(Ka/c)α+(Ka^2/4c^2)-(Ka^2/4c^2)=α^2+(Ka/c)α ∴最初の形:「α^2+*(Ka/c)α」となる!
「 ※ α^2+2☆(Ka/2c)α+★(Ka/2c)^2( =x^2+2☆ax+★a^2 ) 」と表せる!
「 ※ α^2+2☆(Ka/2c)α+★(Ka/2c)^2=(α+☆Ka/2c)^2=(x+☆a)^2!」が完成する! 「※ α^2+(Ka/c)α+(Ka^2/4c^2)-(Ka^2/4c^2) !」となる! 【※ 2次方程式内の、「α^2+*(Ka/c)α」が、因数分解の公式:x^2+2ax+a^2=(x+a)^2 を利用して、平方完成:(α+☆Ka/2c)^2 として成立する事が証明された!】 【α^2+係数2・☆(Ka/2c)・項α+★(Ka/2c)^2 】 ⇔ 【 x^2+係数2・☆a・項x+★a^2 】 ※後は、今までやってきた事を、まとめるだけです! ( 1 ):cα^2+Kaα-Ka=0(c≠0かつ0<α<1) ( 2 ):(c/c)α^2+(Ka/c)α-(Ka/c)=0 ( 3 ):α^2+(Ka/c)α-(Ka/c)=0 ( 4 ):{α^2+2(Ka/2c)α+(Ka/2c)^2}-(Ka/2c)^2-(Ka/c) =0 また、「元の形:α^2+(Ka/c)α」を保つために、「※ (Ka/2c)^2 を差し引いている!」 ( 5 ):(α+Ka/2c)^2-(Ka/2c)^2-(Ka/c)=0 ( 6 ):(α+Ka/2c)^2=(Ka/2c)^2+(Ka/c) ( 7 ):(α+Ka/2c)^2=(Ka^2/4c^2)+(4cKa/4c^2) ( 8 ):(α+Ka/2c)^2=(Ka^2+4cKa)/4c^2 ( 9 ):(α+Ka/2c)^2×^(1/2)={(Ka^2+4cKa)/4c^2 }^ (1/2) ( 10 ):α+(ka/2c)=±√(Ka^2+4cKa)/√4c^2 ( 11 ):α+(Ka/2c)=±√ (Ka^2+4cKa)/√(2^2c^2) ( 12 ):α+(Ka/2c)=±√(Ka^2+4cKa)/√(2c)^2 ( 13 ):α+(Ka/2c)=±√(Ka^2+4cKa)/2c ( 14 ):α=-(Ka/2c)±√(Ka^2+4cKa)/2c ( 15 ): ∴α={-Ka±√(Ka^2+4cKa)}/2c 【 化学での、電離度αを求めるための解の公式 ( 0<α<1 ,より ) 】 ( 16 ) ∴ α={-Ka+√(Ka^2+4cKa) }/2c (c≠0かつ0<α<1) ( 1.):ax^2+bx+c=0(a≠0) ( 2.):(a/a)x^2+(b/a)x+(c/a)=0 ( 3.):x^2+(b/a)x+(c/a)=0 ( 3.)の2次方程式内の、(b/a)x を、因数分解の公式内の、2ax と全く同じ形に変形するために、(2/2)を乗じる事により、係数2が生じ、2(b/2a)xとなる。これより、a=(b/2a)、更に、a^2=(b/2a)^2 だと理解出来る!」つまり、 【 x^2+係数2・a・x+a^2 】 ⇔ 【 x^2+係数2・(b/2a)・x+(b/2a)^2 】 と表せる。これより、 ( 4.):{x^2+2(b/2a)x+(b/2a)^2}-(b/2a)^2+(c/a)=0 「 x^2+(b/a)x{=2(b/2a)x}」 に戻そうと、 「「X」:x^2+2(b/2a)x+(b/2a)^2-(b/2a)^2+(c/a)=0」、としてはならない! 【※ 何故なら、最終的に、xを求めるためには、平方完成の形:因数分解の公式の右辺:(x+a)^2 によって求めなければならないため、上記の様に、(b/2a)^2を差し引いた後の、x^2+2(b/2a)x だけでは、平方完成の形:(x+a)^2 へと導けないからである!】 【 ※ x^2+2(b/2a)x+(b/2a)^2=(x+b/2a)(x+b/2a)=(x+b/2a)^2=(x+a)^2 】 が成立する。よって、この関係式を基にして、次の様に導いていく! ( 5.):「◯」:(x+b/2a)^2-(b/2a)^2+(c/a)=0 ( 6.):(x+b/2a)^2=(b/2a)^2-(c/a) ( 7.):(x+b/2a)^2=(b^2/4a^2)-(c/a)×(4a/4a) ( 8.):(x+b/2a)^2=(b^2/4a^2)-(4ac/4a^2) ( 9.):(x+b/2a)^2=(b^2-4ac)/4a^2 ( 10.): (x+b/2a)^2×^(1/2)={(b^2-4ac)/4a^2}^(1/2) ( 11.): x+(b/2a)=±√(b^2-4ac)/√4a^2 ( 12.):x+(b/2a)=±√(b^2-4ac)/2a ( 13.):x=-(b/2a)±√(b^2-4ac)/2a ( 14.) ∴ x={-b±√(b^2-4ac)}/2a 皆さん、いかがでしょうか?最初で、左辺と右辺に(1/a)を乗じただけで、スッキリした導き方となり、更に理解度が増したのではないでしょうか? この様に、ポイントさえ押さえておけば、すんなりと理解出来ると思いますので、これからも簡単を見過ごさず、1つ1つを丁寧にクリアなさって下さい。 See you ! 2.別解の、 ( 3.)式:x^2+(b/a)x+(c/a)=0 の次式に、左辺の定数項:(c/a)を右辺に移項し、 x^2+(b/a)x=-(c/a)、とした後、両辺に、(b/2a)^2 を足して、 「 x^2+2(b/2a)x+(b/2a)^2=-(c/a)+(b/2a)^2 」 から求めていく解法です! 宜しかったら、すぐ解けますので、計算して試て下さいね!2回目の、 See you !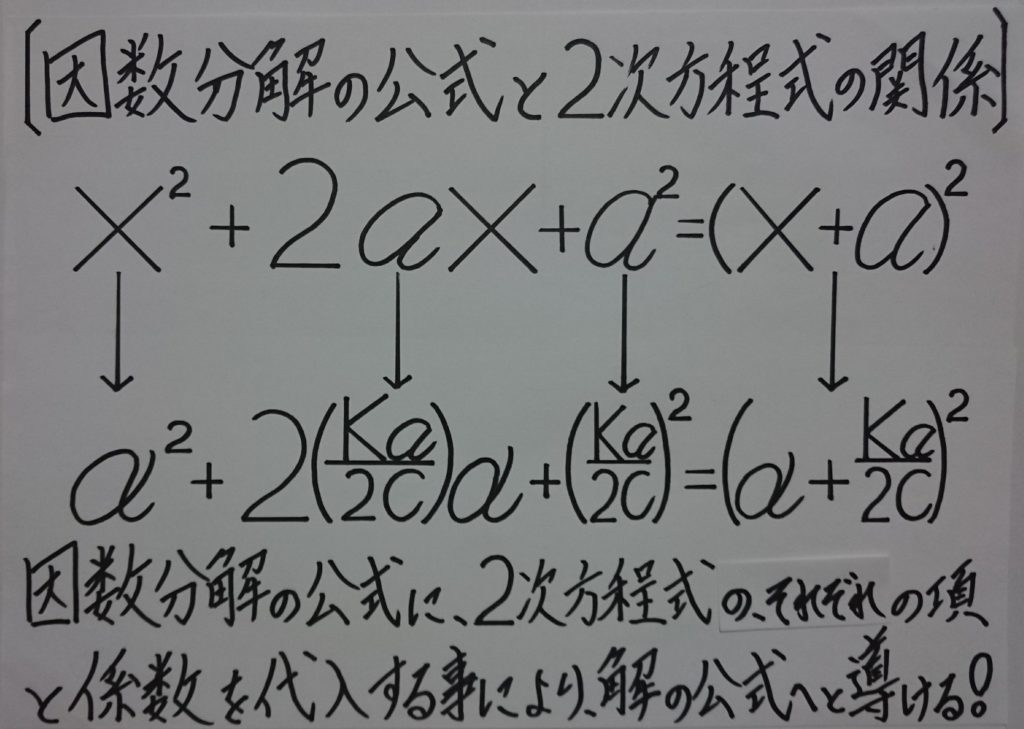
2.別解:一般的な2次方程式からの、解の公式への導き方!














