この記事では中高生の方々を中心に、「まず、最小限pH(ピーエイチ)に必要とされる何を知っておくべきか?」を深く御理解されます様に、「これでもか!」と言う程、最大限細かく解説説明してあります。
今御覧頂いている皆さんは、化学&数学の相互間で、化学に必要とされる数学との共通の公式を上手く活用されているでしょうか?
これから、夢のバケ学として閲覧して頂きます方々には、「千人が千人、答えに辿り着く迄の過程を最重要とし、化学に基礎的な数学を交えながら、一人一人が楽しく学んで御理解出来るモノを提供していく!」事を目標達成とし、一生懸命励んでいきますので、どうぞ宜しくお願い致します!
1.pH(水素イオン指数)は、不思議と人を魅了する!?
 皆さん、初めまして!「夢のバケ学へ、ようこそ!!」。突然ですが、皆さんは「カッコいいー!」って思う人いますか? 私は何故だかpHに関する問題を、スラスラ解ける人が「カッコいいー!」と思ってしまいます。
皆さん、初めまして!「夢のバケ学へ、ようこそ!!」。突然ですが、皆さんは「カッコいいー!」って思う人いますか? 私は何故だかpHに関する問題を、スラスラ解ける人が「カッコいいー!」と思ってしまいます。
皆さんの中にも、何かしらpHの記号:log(ログ)という響きに不思議と魅了され、このように思われる方も僅かながら、いらっしゃるのではないでしょうか?
1―1.pH(水素イオン指数)の計算って、何故難しいの?
ところでpHって、たった2つある[H^+](水素イオン濃度)か、[OH^-](水酸化物イオン濃度)の、いずれかが解れば求める事が可能なのに、どうしてすんなりと解けないのでしょうか?
それは数ある公式を整理仕切れず、公式1つ1つがバラバラになり理解されないまま頭の中に収容されるからだと思います。よって、中でも塩の加水分解では特に、収容された公式を応用化出来ずじまいの結果に成り易いでしょう。
弱酸を初め、pHを制覇するには基礎的な数学の公式が必須になりますので、皆さんが公式1つ1つに、ゆっくり時間を掛け必ず理解された後、次の段階へと進むようにして下されば幸いです。
それでは、今まで皆さんが理解に苦しんで、痒い所まであと一歩が届かなかったものへと挑んで行きましょう!
2.解の公式を理解しよう!
「何故、解の公式?」って思われるでしょうが、解の公式にはpHを求めるための重要な基礎的要素が多く含まれています。化学も基礎的分野を落としたら、ズルズルと全く解らない方向へと進んでしまう教科だと思います。
ですから基礎となる要素を、しっかりと理解して頂きたくて、あえてトップに持って来ました。中でも、文字による解の公式は「覚えたら忘れるを繰り返す人が多数いる」のではないでしょうか?
2-1.モル濃度c 〔mol/L〕、弱酸の電離度α、電離定数Ka〔mol/L〕から、2次方程式を求めてみよう!
「前代未聞!?弱酸のpH&pOHを制覇する術(すべ)、此処に在り!」
「前代未聞!?弱塩基のpH&pOHを制覇する術、此処に在り!」
の記事の方を是非とも御覧下さい。
また、「解の公式」、「pHは、水素イオン濃度[H^+]の逆数の常用対数?」、「累乗根と常用対数」について、
の方にも、この記事との関係性が詳しく記載してありますので、宜しかったらこちらも是非御覧下さい!
よって、α≒0でない場合、1-α≒1と出来ない事から、
1.)Ka〔mol/L〕=c^2α^2/c(1-α) =(c×c×α^2)/c(1-α)=cα^2/1-α
つまり、「 Ka=cα^2/1-α 」 より、2次方程式を完成させていきます。
2.)上式の左辺と右辺を入れ替え、cα^2/1-α=Ka より、左辺の分母である1-αを消去するために、両辺に(1-α)を乗じると、
「(cα^2/1-α)×(1-α)=Ka×(1-α) 」
→「 cα^2=Ka-Kaα 」
3.)右辺を左辺に移項すると、
cα^2+Kaα-Ka=0
2次方程式が成立します!
2-2.☆ 2次方程式から、解の公式を導こう!
そのために、「※ Kaαのαを消去し、cα^2内のα^2を、α^2=解(答)」、という方向へと導いていく必要があります!
【※ 要は、この☆cα^2+Kaαと、全く同じ意味を持つ式を繋げていけば良い!】のです。それにはまず、左辺の「cα^2の係数であるc」を用いて、「☆cα^2+Kaαと全く同じ式を成立させていく事が最重要!」になります!
( 1.)「 cα^2+Kaα-Ka=0 :[1]」
→「 c(α^2+Ka/c・α)-Ka=0 :[2]」(※ Ka/c・α=(Ka/c)α)
「 c(α^2+Ka/c・α)-Ka=0:[2]」
→「 c×α^2+c×(Ka/c)α-Ka=0 」
→ 「☆cα^2+Kaα-Ka=0 」
( 2.) 「 c{(α+Ka/2c)^2-(Ka^2/4c^2)}-Ka =0 :[3]」
→「 c{(α+Ka/2c)(α+Ka/2c)-(Ka^2/4c^2)}-Ka=0 」
→「 c{α^2+(Ka/2c)α+(Ka/2c)α+(Ka^2/4c^2)-(Ka^2/4c^2)}-Ka=0」
→「 c{α^2+2(Ka/2c)α+(Ka^2/4c^2)-(Ka^2/4c^2)}-Ka=0」
→「 c {α^2+(Ka/c)α+(Ka^2/4c^2)-(Ka^2/4c^2)}-Ka=0」
更に、「☆α^2+(Ka/c)α」によって、(α+Ka/2c)^2といった平方(2乗)が完成し、これから(Ka^2/4c^2)を差し引いた式が、元の式である、α^2+(Ka/c)αと全く同じ式になります。つまり、
「☆α^2+(Ka/c)☆α=(★α+Ka/2c)^2-(Ka^2/4c^2)」と、表せます!
この左式と右式との関係式で気付くべき点は、「※左式では☆αが、☆α^2と(Ka/c)☆αの2箇所に置かれているものが、※右式では2個の☆αが、★α1個に変化している!」という点です!
これは左式の(Ka/c)αに、(1/2)乗じる事により(※あえて、ここでは、(1/2)を乗じるとαが外れる、としています。「※ 実際には、因数分解の公式を利用して、(2/2)を乗じ、2(Ka/2c)αの形にする事によって平方(2乗)が完成し(後述しています)、左式で2個だったαから、右式の平方(2乗)では、余計なαが1個消去され、最終的には、「左辺のα=解」という様に、電離度αが導き易くなっています!」
それは、「上記☆右式の(α+Ka/2c)^2を、(α+Ka/2c)(α+Ka/2c)の因数分解の形にしてから2次方程式を完成させる!」といった性質を上手く利用する事で全く同じ式が完成する、といった仕組みになっているからです!】
2-3.☆ ここが鍵(カギ)!2次方程式を、因数分解の公式の性質を利用し、解いてみよう!
([1][2]:4X [2′][3]:☆+1)([1][2′]:5X [2][3]:★-1)=0
【※ 2次方程式が完成する手順!】
(Ⅰ):[1]×[1]=4X×5X=20X^2
(Ⅱ):[2]×[2]+[2′]×[2′]=4X×(★-1)☆+1×5X=-4X+5X=1X(係数1を省略して)=X
(Ⅲ):[3]×[3]=☆+1×(★-1)=-1
∴[1]×[1]、[2]×[2]+[2′]×[2′]、[3]×[3]より、2次方程式:20X^2+X-1=0 成立!
つまり、この☆+1と、★-1は、(Ⅱ)と(Ⅲ)による計算式に用いますから、両辺の計算式を満たす符号(+、-)を含んだ値に、必ずなるように出来ています。これを踏まえて、本題の式が成立する様に因数分解を展開し、2次方程式が完成する過程として上式に当てはめて試ましょう!
=(α+Ka/2c)(α+Ka/2c)-(Ka^2/4c^2)
([1][2]:α +[2′][3]:☆Ka/2c) ([1][2′]:α +[2][3]:★Ka/2c)-(Ka^2/4c^2)
【※ 手順】
(!):[1]×[1]=α×α=α^2
(Ⅱ):[2]×[2]+[2′]×[2′]=(α×★Ka/2c)+(☆Ka/2c×α)
=(★Ka/2c)α+(☆Ka/2c)α
=2(Ka/2c)α
=(Ka/c)α
(Ⅲ):[3]×[3]=(☆Ka/2c)×(★Ka/2c)=(Ka^2/4c^2)
∴これにより、「 (α+Ka/2c)^2が、2次方程式:α^2+(Ka/c)α+(Ka^2/4c^2) に展開 !」されます。
また、この2次方程式が、α^2+(Ka/c)αと同じ式として成立するためには、「※ (Ⅲ):[3]×[3]の(Ka^2/4c^2)が余計な値として式に加わっており、下記の様にこれと全く同じ値*(Ka^2/4c^2)を差し引く!」事で、α^2+(Ka/c)αと全く同じ式が出来上がります。
「※ α^2+(Ka/c)α+(Ka^2/4c^2)-*(Ka^2/4c^2)=α^2+(Ka/c)α」
いかがでしょうか?2次方程式から解の公式が完成するために、最も重要な仕組みが判明しました!
これから最終段階である、( 2.)の[3]式の、c{(α+Ka/2c)^2-(Ka^2/4c^2)}-Ka=0より、電離度αを求めていきましょう!
(α+Ka/2c)^2=α^2+2(Ka/2c)α+(Ka/2c)^2(=Ka^2/4c^2)
でもあるため、※因数分解の公式:x^2+2ax+a^2=(x+a)^2を応用化している!】
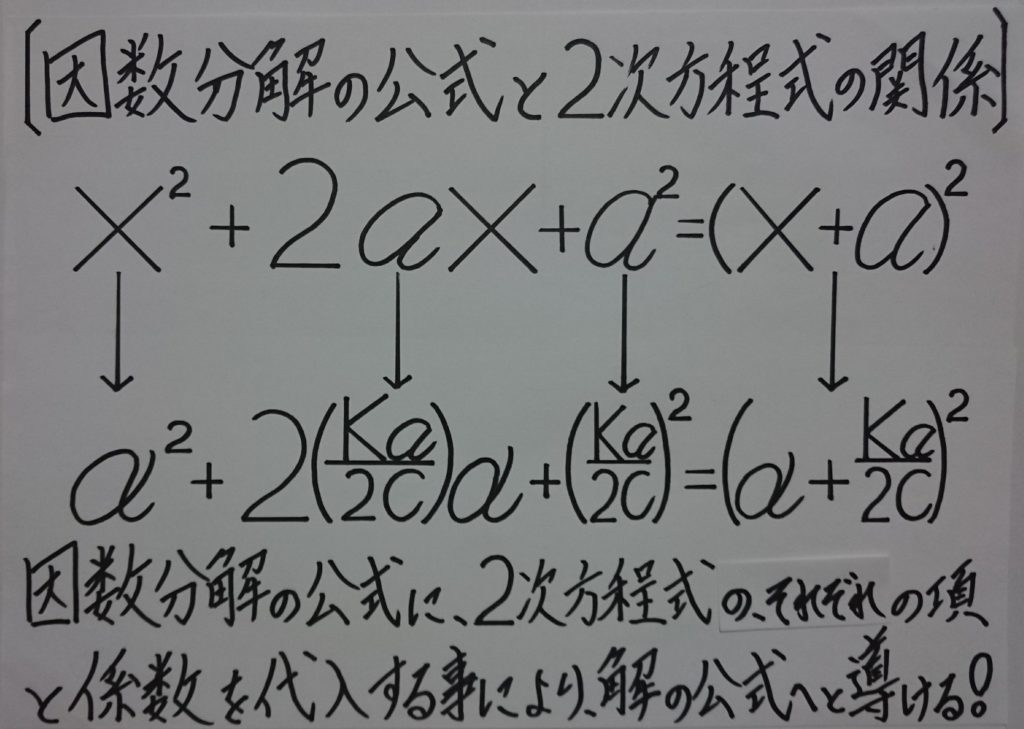
∴ 【 x^2+2ax+a^2=(x+a)^2⇔α^2+2(Ka/2c)α+(Ka/2c)^2=(α+Ka/2c)^2 】
( 1.)cα^2+Kaα-Ka=0(c≠0かつ0<α<1)の場合と、( 2.)一般的な2次方程式:ax^2+bx+c=0(a≠0)
の場合の2式を紹介してあります。皆さんの理解度が、更に深まると思いますので、宜しかったら、そちらの方も是非御参照下さい!】
3. 係数の性質と、係数cの役割!
[1]:(4X+1)=0、[2]:(5X-1)=0 より、
[1]:4X+1=0 → 4X=-1 ∴ X=-(1/4)
[2]:5X-1=0 → 5X=1 ∴ X=(1/5)
[ 1.]X+X=(係数1+係数1)X=(1+1)X=2X 〔X+Xのような、係数のないXによる計算式の場合、係数1は元々省略されている!〕
[ 2.]7X+7X=(係数7+係数7)X=(7+7)X=14X
[ 1.]X-X=(係数1-係数1)X=(1-1)X=0
[ 2.]10X-5X=(係数10-係数5)X=(10-5)X=5X
[ 1.]X×X=(係数1×係数1)×X×X=1×X^(1+1)=X^2
[ 2.]3X^2×4X^3=(係数3×係数4)×X^2×X^3=(3×4)×X^(2+3)=12X^5
さて、この辺で元に戻りましょう。
さて、この式中で着目するのが、係数☆cの存在になりますが、何故(α+Ka/2c)^2ばかりでなく、「★-(Ka^2/4c^2)まで、係数☆cが乗じてある!」のでしょうか?
それは、「※ 最初に着目した式:cα^2+Kaαの式」が、
「 c{(α+Ka/2c)^2-(Ka^2/4c^2)}」
までの式と、全く同じ意味を持つからです!
【※ cα^2+Kaα=c{(α+Ka/2c)^2-(Ka^2/4c^2)}=両式とも全く同じ意味を表している式!】である。
( 3.)「※ c{(α+Ka/2c)^2-(Ka^2/4c^2)}」の式を、(α+Ka/2c)^2のみが、係数cと乗じ合い、次の様な誤った式を立てない様に注意しましょう!
「X」:c(α+Ka/2c)^2-(Ka^2/4c^2)
正しくは、「※ c{(α+Ka/2c)^2-(Ka^2/4☆c^2)}-Ka=0」 より、
「◯」:c(α+Ka/2c)^2-(Ka^2/4☆c)-Ka=0
つまり、「※ (α+Ka/2c)^2には、係数cを乗じて、c(α+Ka/2c)^2の状態のままの式!」にしておき、「※ 最終的には、この(α+Ka/2c)^2により、電離度αは求められる!」という事になります。
よって、ここでは、「-(☆Ka^2/4c^2)だけに、係数cを乗じ、互いにcを消去し合い、-(Ka^2/4☆c)と、分母:4c^2のcが1個減少します!」
そして、「c(α+Ka/2c)^2の式は、まだ係数cと、(α+Ka/2c)^2が乗じ合っているので、この式のまま残しておきます!」
次にαを求めるために、左辺にαが残っている式を残し、左辺:-(Ka^2/4c)-Ka を右辺に移項し、-(マイナス)だった符号を+(プラス)の符号にし、右辺:(Ka^2/4c)+Ka の式が成立する!
( 5.)「 ☆c(α+Ka/2c)^2=(Ka^2/4c)+(4cKa/4c) 」
→ 「 ☆c(α+Ka/2c)^2=(Ka^2+4cKa)/4c 」
→ 「※ (α+Ka/2c)^2=(Ka^2+4cKa)/4☆c^2 」
*( 4.)の右辺を、更にまとめるために、右辺の分数である(Ka^2/4c)に、Kaを合わせる。(Ka^2/4c)の分母である4cを、(4c/4c)として、Kaに乗じると、(4c/4c)×Ka=(4cKa/4c)となる。
理由として、この時のKa自体は、(Ka/1)=Kaより、(Ka/1)つまり、分子であるKaを指し、1が分母を指している。よって、(Ka^2/4c)の分母4cは、分子であるKaにも、分母である1にも乗じなければならないからである!
∴ (4c/4c)×(Ka/1)=(4c×Ka)/(4c×1)=(4cKa/4c)
これで、いよいよ計算も終盤になって来ました。ここで、最後にαを導く邪魔をしている「☆係数cを、左辺から消去するために、係数cを右辺に移項します。この時cは、逆数である(1/c)となって、右辺である(Ka^2+4cKa)/4cに乗じます(10の逆数=1/10=0.1=10^(-1) 等と同じ考え方です。)!
「 ☆c(α+Ka/2c)^2=(Ka^2+4cKa)/4c 」
→ 「(α+Ka/2c)^2=(Ka^2+4cKa)/4c×(1/☆c) 」
∴(α+Ka/2c)^2=(Ka^2+4cKa)/4☆c^2
3-1.指数(1/2)の役割と、累乗根(=平方根=2乗根)の扱い方。
→ 「 α+(Ka/2c)=±√(Ka^2+4cKa)/√4c^2 :[5]」
→ 「α+(Ka/2c)=±√(Ka^2+4cKa)/√(2^2c^2) 」
→ 「α+(Ka/2c)=±√(Ka^2+4cKa)/√(2c)^2 」
→ 「α+(Ka/2c)=±√(Ka^2+4cKa)/☆2c 」
→ 「α=-(Ka/2c)±√(Ka^2+4cKa)/☆2c 」
∴α={-Ka±√(Ka^2+4cKa)}/2c
それには、まず、左辺の( )^2を外してやる必要があります。「この( )^2を外す作業が、両辺に(1/2)を指数として乗じる事!」なのです。これにより、「左辺のαと、(Ka/2c)とを切り離す」事が出来ます。そして、両辺に乗じてある指数(1/2)こそが最も重要な存在になっています。同時に両辺に乗じてある(1/2)乗に加え、更に累乗根が深く関わっています。
それでは、特に複雑である右辺から考えていきましょう。( 6.)の[4]式の右辺:「※{(Ka^2+4cKa)/4c^2}^(1/2)」は、累乗根の最も基礎的な式になっています。この式には、「累乗根の定義」が本質的に大きく関わっています。ここからは、この累乗根(=平方根=2乗根)を用いて解の公式へと導いて行きます。
【 {(Ka^2+4cKa)/4c^2}^(1/2) :[4]
=±√(Ka^2+4cKa)/√☆4c^2 :[5]
=±√(Ka^2+4cKa)/√(☆2^2c^2)
=±√(Ka^2+4cKa)/√☆(2c)^2
=±√(Ka^2+4cKa)/☆2c 】
⇔【 a^(1/2)=±√a より、どちらの式もnが偶数乗根、つまり、2乗根=平方根を表している!】
⇔【※(例): 16^(1/2)=±√16=±√4^2=±4^(2/2)=±4 】
〔※ ( 6.)の[4]式の左辺と右辺に、指数(1/2)乗を表している、^(1/2)等は、( )を外して、^1/2としてお考え下さい。また、[5]式等、2つの√が分子・分母に記述してある式は、本来1個の√であると、お考えご使用下さい!〕
お気付きでしょうか?( 6.)の[4]式の右辺だけをまとめた式は、別参照の「 nが、偶数乗根(ここでは、n=2)だった場合と全く同じ!」なんです。つまり、これ等の式は、「2乗根=平方根」を表しているのです(※ 化学のpHも、2乗根=平方根によって求められます)!
そして、ここで注目すべきが☆の付いている「分母の部分☆4c^2」です。更に当然、2乗根(=平方根)√は、
「±√(Ka^2+4cKa)/√☆4c^2」
の、分子と分母の両方に通じている事にも注目します!
分子である√(Ka^2+4cKa)は、これ以上簡単にする事は出来ませんが、分母である√(☆4c^2) は、
「√(4c^2)=√(2^2c^2)==√(2c)^2=(2c)^(2/2)=2c」
という様に、2cまで簡単にする事が出来るのです!
※ 累乗根は、この様に中々気付きにくい所まで入り込んでいますが、上記の様に細かく分解していけば理解し易くなったのではないでしょうか?ここまでくれば後はスムーズに解いていけます。
( 6.)の[4]式の「左辺:(α+Ka/2c)^2×^(1/2)=α+(Ka/2c)」
の様に左辺に(1/2)乗すると( )が外れます。ここで上記の右辺と一緒にまとめると、
「α+(Ka/2c)=±√(Ka^2+4cKa)/2c」
となり、これよりαだけを求めるために、左辺の(Ka/2c)を右辺に、-(Ka/2c)として移項すれば次の様にまとまります。
「α=-(Ka/2c)±√(Ka^2+4cKa)/2c」
右辺の2つの分母は、どちらとも2cで同じですので、これをまとめると最終的に、
「∴α={-Ka±√(Ka^2+4cKa)}/2c」
が、完成します(※ 計算等には、{ }を外した解の公式として御利用下さい)!
また、「※ 電離度αは、通常、0<α<1を満たす事から(モル濃度:c〔mol/L〕×α=cα〔mol/L〕 は、正であり、負ではない、という意味)、符号:マイナス(-)が公式から除外され、プラス(+)のみが公式内に残り、最終的に電離度αは次式によって求められる!」
【 α={-Ka☆+√(Ka^2+4cKa)}/2c 】
ちなみに、2次方程式:ax^2+bx-c=0(a≠0)により、xを求める場合には、「解の公式:x={-b±√(b^2+4ac)}/2a(a≠0)」に、「2次方程式の、項x^2の係数a、項xの係数b、定数項cの、それぞれの値を、解の公式の同じ文字に、値として代入しなければならない!」
※最後に、解の公式が求められる迄の一連の流れをまとめてみました。
3-2.まとめ:解の公式の整理式!
(2):c(α^2+Ka/c・α)-Ka=0
(3):☆c{(α+Ka/2c)^2-(Ka^2/4c^2)}-Ka=0
(4):c(α+Ka/2c)^2-(Ka^2/4☆c)-Ka=0
(6):c(α+Ka/2c)^2=(Ka^2/4c)+(4cKa/4c)
(7):c(α+Ka/2c)^2=(Ka^2+4cKa)/4c
(9):(α+Ka/2c)^2×^(1/2)={(Ka^2+4cKa)/4c^2}^(1/2)
(11):α+(Ka/2c)=±√(Ka^2+4cKa)/√(2^2c^2)
(12):α+(Ka/2c)=±√(Ka^2+4cKa)/√(2c)^2
(14):α=-(Ka/2c)±√(Ka^2+4cKa)/2c
【 α={-Ka☆+√(Ka^2+4cKa)}/2c 】
皆さん、永々とお付きあい頂きまして誠に有り難うございました。最後になりますが、これから先皆さんが様々なパターンのpHを求めていくのに最低限必要な事は、数学による基礎的勉学が必須だという事です。
特に手こずるであろうのが、「塩の加水分解」でしょう。塩の加水分解は、弱酸及び弱塩基の真逆的性質を持ち合わせているために、難問の1つとして存在しているのではないでしょうか?ですが、加水分解の持つ性質さえ理解すれば、基礎的要素から解く事が可能になります。勿論、この場合にもlog(ログ)や、累乗根等の基礎的勉学が必ず必要になってきます。
「解けるかな?出来るかな?」って思われている方、どうか「ウルトラ御安心!」下さい。「弱酸、弱塩基同様に全体像の観える公式的なものを利用!」すれば、答えが導かれる迄の問題を解くために必要な過程の流れが、はっきりと理解出来ます。
この公式的な公式と言うのは、私自身が勝手に創造したものですが、皆さんにとっては、「すぐに、この公式的なものが理解出来、いつまでも皆さんの頭の中に残り続け、そして、いつでも引き出せるもの」になってくれると信じています。
この記事の続編と致しまして、徐々にですが御紹介していきたいと思いますので、是非御覧下さい。また今回の別解と致しまして、「一目瞭然!2次方程式から、解の公式を導く方法!」の方では、今回より更に理解度が増すかと思われますので、宜しかったらこちらも御覧頂けたらと思います。本日はお付き合い下さいまして、誠に有り難うございました。それでは、 See you !













