皆さん、いつもお世話になっています!
今回は、わたくし若輩者ですが、「❋ ヘンリーの法則!」について記事を書いて試ました。私事ですが最初は正直、参考書等読んでも全く理解出来ませんでした。
そうです、「Oh,My God!Help me!」状態だったんです!しかし解らなかったこそ、今は皆さんが、仮に理解するのに少々手こずっているとしたら、一体何処に一番頭を使っているのかを予測出来るのではないかと思っています。
それでは、目に観えない気体の溶解度を中心に、ヘンリーの定義を1つ1つイメージ解釈しながらズバッと解決していきましょう!
1.ヘンリーの法則を考察してみよう!

まずはヘンリーの法則をおさらいしてみましょう。
当たり前ですが、本来ヘンリーの法則は定義として書されていますが、ヘンリーの法則を扱っている参考書等では、意味は同じでも書き方としては様々な扱い方がしてあります。
ここでも私なりの解釈でヘンリーの法則を文章化してみたいと思います。
[1]〔❋ 物質量と圧力の関係〕;「水に溶解する気体の物質量〔mol〕は、気体の圧力(分圧)、水の量に比例する!」
[2]〔❋ 体積と圧力の関係!〕;「水に溶解する気体の体積は圧力に関わらず(❋ その時その時に加えた気体の圧力下において!)変化せず一定となる!」
この[1]については、「❋ 圧力を高くしたら、物質量〔mol〕も圧力(分圧)と水の量に比例して増加する、つまり、押す毎(ごと)に気体が溶ける量も増えていく!」の様に理解しやすいのですが、問題は[2]です。
[1]では比例する、[2]では一定である、といった様に、たった2つしかないヘンリーの法則の意味が[2]で一気に解らなくなってきます。
私が最初に立ち止まったのが、この[2]「❋ 気体の体積は一定となる、つまりいくら圧力をかけようが、気体の体積は最初に圧力をかけた時の体積から一切変化しない!」でした!
おそらく皆さんが頭を傾(かし)げるとしたら、この[2]ではないでしょうか?確かに理解もイメージもしづらい箇所ではありますね。
そこでヘンリーの法則の[2]は、とにかく理解しにくいと考えられますので、次の様な図に表したものでイメージして頂けたらと思います!
2.ヘンリーの法則を図で理解イメージしてみよう!
ここではヘンリーの法則の[2]を図で表しています。皆さん、それぞれのイメージをされたらと思います。
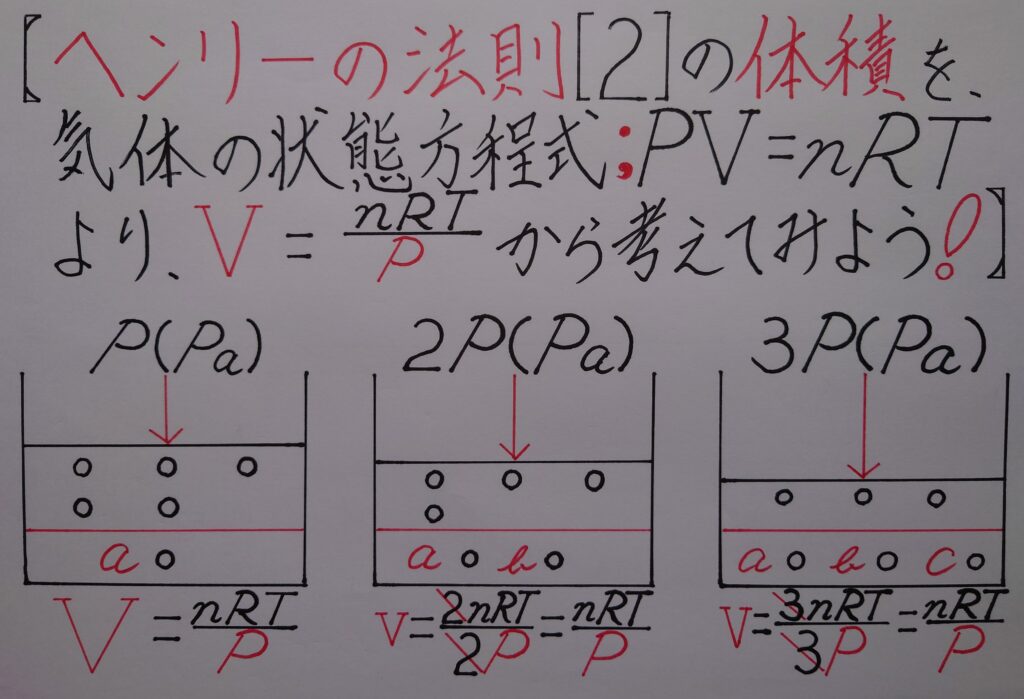

上の画像は圧力に応じて水に溶解した気体の体積V〔L〕は一定である状態を図にしたものです。
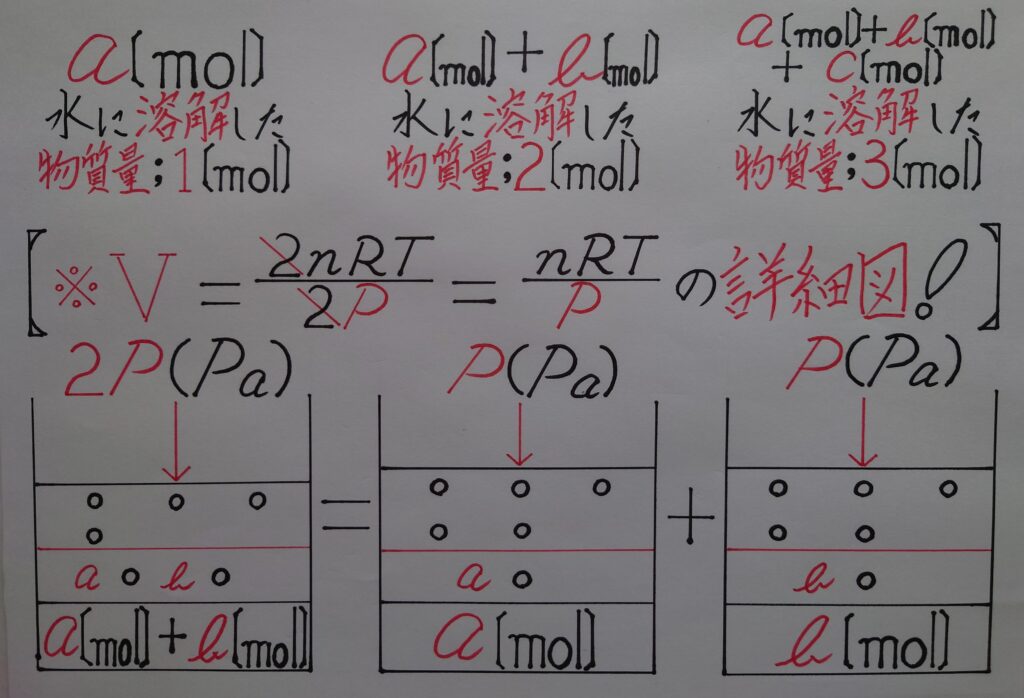
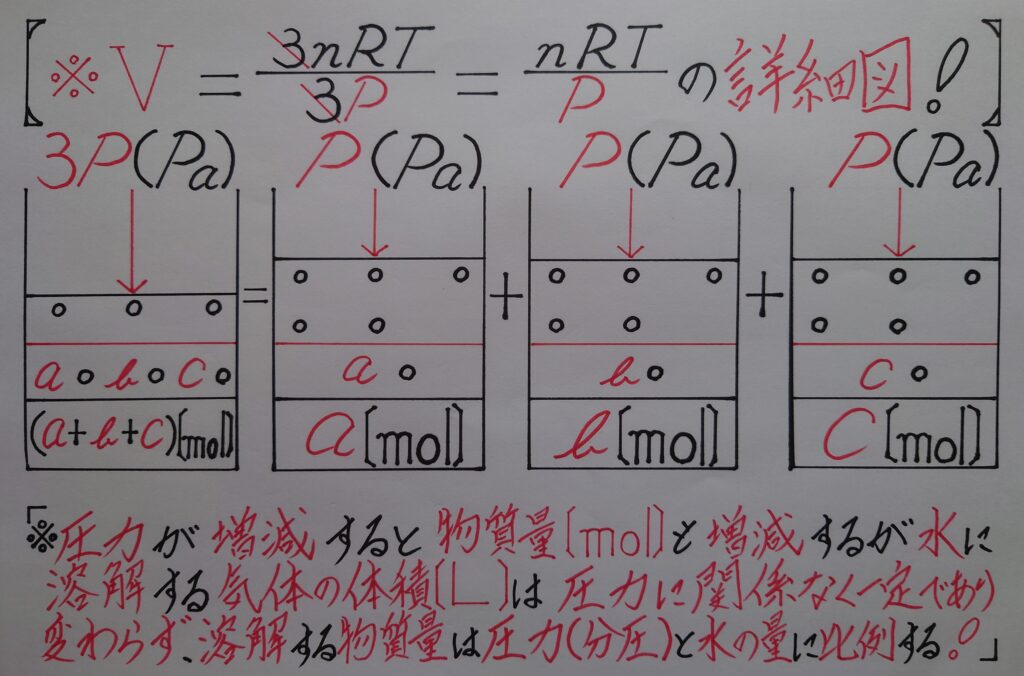
しかし、2枚目の画像に体積V〔L〕が2通り書いてあります。1番目の体積V〔L〕は「❋ 気体の状態方程式!」によってイメージ出来ますが、2番目の体積V〔L〕は何故圧力に比例して増加しているのか、理解しづらいのではないでしょうか?
通常、圧力が上がる毎に物質量〔mol〕は増加し、体積V〔L〕は一定なのですが、仮に水に溶けている一定である体積V〔L〕の気体を取り出せるものとして、その気体の量を標準状態で計測すると、
【❋ 圧力が解(ほど)けた状態(圧力がかかってない状態!)になっている為に、本来の気体の物質量〔mol〕の体積V〔L〕になる!】という事になります!
こちらの一定とはならない体積V〔L〕につきましては、後程の問題文によって理解イメージされる事をお勧めします。
つまり、物質量が2倍かつ体積が2倍になった状態を、同じ2倍の圧力で押し戻している為に体積は変化しないイメージ(❋ 3倍、4倍、〜倍の圧力を加えても、気体の体積は全く変わらないという考え方は同じであるという事!)されたら理解しやすいのではないでしょうか!
皆さん、うまくイメージ出来たでしょうか?さらに理解度を向上させる為に、ここからは幾つか問題文を解いていきましょう!
3.ヘンリーの法則を問題文で攻略しよう!
ここからは問題文によってヘンリーの法則を理解して頂きたいと思います。
です。まずは、物質量〔mol〕を中心に問いていく事をお勧め致します。
そして物質量〔mol〕も重要なんですが、こちらも影に隠れた立役者として最重要なんです!それが、
です。この対比は、よく化学で取り扱われます。ヘンリーの法則でも重要なポジションとして存在しています。ですので、「❋ 物質量〔mol〕と対比!」に着目して頂けたらと思います。
問題文を1つずつ理解しながら解いていかれますと、ヘンリーの法則がどういった法則かが解ってくるはずですので、どの様な問題にも対応出来ます様に、ランダムではありますが問題文を解いていかれたらと思います!
それでは、問題を問いていきましょう。
(✕)︰まずO2とN2の分圧を求める!
の様に解き始めると「アウト!」になります。ということは、この問題に「混合気体の比は使用しない!」ことになります。
問題文の中で重要な文章は、「❋ この水量に応じた圧力下における体積〔L〕」であり、つまり、「❋ 一定の条件下においての体積〔L〕」であるから、「❋ 0℃、1.0✕10^5Pa下の水1.0Lを基準にし、酸素と窒素がそれぞれ水5.0Lに溶解する体積〔L〕を求める!」ということになります。よって、求める体積〔L〕は、
O2の体積︰30mL✕5(=5L)=150mL=1.5✕10^-1L 答.0.15〔L〕
N2の体積︰15mL✕5(=5L)=75mL=7.5✕10^-2L 答.0.075〔L〕
となります。因みに、混合気体の比を使用する場合には、「❋ (ある水の量に)溶解する気体の体積を標準状態(❋ 0℃、1.0✕10^5Pa)に換算した!」、「水1.0Lに空気(酸素、窒素などで、空気という言葉が混合気体を表している場合!)が接触しているとき!」と、いう様な文章が盛り込まれると思いますので、ヘンリーの法則をさらに理解する上での目安となるのではないでしょうか。
(1)20℃、1.0✕10^5Pa下で水5.0Lに6.5✕10^-3molの酸素が溶解しているとき、接水している気体のO2の圧力は何Paか。
(2)20℃、水10Lに3.0✕10^5PaのO2が接しているとき、水に溶解しているO2の物質量〔mol〕と質量〔g〕を求め、N2に関しては質量〔g〕を求めよ。
(3)20℃、水5.0Lに1.0✕10^5Paの空気が接しているとき、水に溶解しているO2の物質量とN2の物質量を求めよ。また、水に溶解しているN2の物質量はO2の物質量の何倍かも求めよ。
(1)20℃、1.0✕10^5Pa下で水5.0Lに6.5✕10^-3molの酸素が溶解しているとき、接水している気体のO2の圧力は何Paか。
まず、酸素と窒素が水1.0Lに溶解している物質量〔mol〕を求めると、
O2の物質量〔mol〕︰(3.0✕10^-2L)/(22.4L/mol)=1.3✕10^-3mol
N2の物質量〔mol〕︰(1.5✕10^-2L)/(22.4L/mol)=6.7✕10^-4mol
(1.3✕10^-3mol)✕(xPa/1.0✕10^5Pa)✕(5.0L/1.0L)=6.5✕10^-3mol
(1.3✕10^-3mol✕xPa✕5.0L)/(1.0✕10^5Pa✕1.0L)=6.5✕10^-3mol
(6.5✕10^-3x)/(1.0✕10^5)=6.5✕10^-3mol
6.5✕10^-8x=6.5✕10^-3
x=1.0✕10^5Pa 答.1.0✕10^5Pa
(2)20℃、水10Lに3.0✕10^5PaのO2が接しているとき、水に溶解しているO2の物質量〔mol〕と質量〔g〕を求め、N2に関しては質量〔g〕を求めよ。
圧力が3倍の3.0✕10^5Pa、物質量〔mol〕は水の量10Lに比例するから、
O2の物質量〔mol〕︰1.3✕10^-3mol✕3✕10=3.9✕10^-2mol 答.3.9✕10^-2mol
O2の質量〔g〕︰3.9✕10^-2mol✕32〔g/mol〕=1.248g 答.1.25〔g〕
N2の質量〔g〕︰6.7✕10^-4mol✕3✕10✕28〔g/mol〕=0.5628g 答.0.56〔g〕
この(2)の問題などはヘンリーの法則に付き物ですが、分圧を扱う問題ではないことに着目して下さい。つまり、【❋ 混合気体の分圧が記されているからといって、全ての問題に分圧の計算が必要とは限りません!分圧の計算が必要でない問題も、あたかも必要な様に問題が出されています!ここが皆さんを惑わしている重要なポイントでもありますので、気体の分圧と、気体の分圧ではない問題の区別とを理解しておきましょう!】
酸素と窒素の分圧を求めると、
O2の分圧︰1.0✕10^5Pa✕(1/5)=2.0✕10^4Pa
N2の分圧︰1.0✕10^5Pa✕(4/5)=8.0✕10^4Pa
酸素と窒素の物質量〔mol〕に水5.0L(溶解した気体は水の量に比例する!)と分圧を乗じると、
O2の物質量〔mol〕︰(3.0✕10^-2L/22.4L/mol)✕5(L)✕(2.0✕10^4Pa/1.0✕10^5Pa)=1.3✕10^-3mol
N2の物質量〔mol〕︰(1.5✕10^-2L/22.4L/mol)✕5(L)✕(8.0✕10^4Pa/1.0✕10^5Pa)=2.7✕10^-3mol
(2.7✕10^-3mol)÷(1.3✕10^-3mol)≒2.08 答.2倍
1.4✕10^-3mol✕(3.0✕10^5Pa/1.0✕10^5Pa)✕(3L/1L)=1.4✕10^-3mol✕3✕3=0.0126mol 答.0.013〔mol〕
(1)0℃、1.0✕10^5Pa下で、水1.0Lに溶解する窒素と酸素の体積を答えよ。
(2)0℃、3.0✕10^5Paの窒素が水1.0Lと接しているとき、水に溶解する窒素の質量は何gか。
(3)(2)より、0℃、3.0✕10^5Pa下での窒素の体積を答えよ。
(4)0℃、1.0✕10^5Paの空気が水1.0Lと接しているとき、水に溶解する窒素と酸素の質量は何gか。ただし、空気は窒素と酸素の体積比が4︰1の混合物であり、N2=28、O2=32とする。
(5)(4)の窒素と酸素の混合気体を0℃、1.0✕10^5Pa下で水3.0Lに接触させたとき、[a]溶解している窒素と酸素の量を標準状態下での気体の体積比を小数第1位まで求め、[b]それぞれの分圧による窒素と酸素の体積比も求めよ。
(1)0℃、1.0✕10^5Pa下で、水1.0Lに溶解する窒素と酸素の体積を答えよ。
N2とO2が水1.0Lに溶解する体積は、1000倍すればいいから、
N2の体積︰0.023mL✕1000=23mL 答.23mL
O2の体積︰0.049mL✕1000=49mL 答.49mL
(2)0℃、3.0✕10^5Paの窒素が水1.0Lと接しているとき、水に溶解する窒素の質量は何gか。
(23mL✕10^-3L/mL)/(22.4L/mol)✕28〔g/mol〕✕(3.0✕10^5Pa/1.0✕10^5Pa)=0.023L/(22.4L/mol)✕28〔g/mol〕✕3=0.08625g 答.0.086〔g〕
(3)(2)より、0℃、3.0✕10^5Pa下での窒素の体積を答えよ。
温度一定で体積は圧力に関係なく一定なので、0℃で、圧力1.0✕10^5Paが3.0✕10^5Paに増加しても、水1.0Lに溶解する気体の体積は変わらず、
答.23mL
(4)0℃、1.0✕10^5Paの空気が水1.0Lと接しているとき、水に溶解する窒素と酸素の質量は何gか。ただし、空気は窒素と酸素の体積比が4︰1の混合物であり、N2=28、O2=32とする。
(1)で求めたN2とO2の体積と、分圧の比が、N2=(4/5)、O2=(1/5)を利用します。
N2の質量︰(23mL✕10^-3L/mL)/(22.4L/mol)✕28〔g/mol〕✕(4/5)=0.023g 答.0.023〔g〕
O2の質量︰(49mL✕10^-3L/mL)/(22.4L/mol)✕32〔g/mol〕✕(1/5)=0.014g 答.0.014〔g〕
(5)(4)の窒素と酸素の混合気体を0℃、1.0✕10^5Pa下で水3.0Lに接触させたとき、[a]溶解している窒素と酸素の量を標準状態下での気体の体積比を小数第1位まで求め、[b]それぞれの分圧による窒素と酸素の体積比も求めよ。
[a]標準状態で、窒素と酸素は分圧によって存在していることから、それぞれの分圧を求めると、
窒素N2の分圧︰1.0✕10^5Pa✕(4/5)
酸素O2の分圧︰1.0✕10^5Pa✕(1/5)
(1)で水1Lに溶解している窒素と酸素の体積より3.0L分の体積を求めると、
N2の体積︰23mL✕(4/5✕1.0✕10^5Pa/1.0✕10^5Pa)✕(3.0L/1.0L)=55.2mL
O2の体積︰49mL✕(1/5✕1.0✕10^5Pa/1.0✕10^5Pa)✕(3.0L/1.0L)=29.4mL
55.2mL︰29.4mL=9.2︰4.9 答.(N2)9.2︰(O2)4.9
[b]窒素と酸素の全圧(分圧)は、それぞれ1.0✕10^5Paであり、1.0Lを基準とした水にどのくらいの気体が溶解しているかなので、気体は3.0L分溶解するので、それぞれの体積に3.0Lを乗じるだけです。
N2の体積︰23mL✕(3.0L/1.0L)=69mL
O2の体積︰49mL✕(3.0L/1.0L)=147mL
答.(N2)23︰(O2)49
3.0✕10^5Pa✕0.018L=1.0✕10^5Pa✕xL
3.0✕10^5✕0.018=1.0✕10^5x
x=0.054L 答.0.054L
3.0✕10^5Paで水素H2は水1.0Lに0.018L溶けます。これは体積は圧力に関係なく一定であるためです。これと反比例して物質量〔mol〕は水1.0Lに3倍溶けています。
この圧力を1.0✕10^5Paに落とすと、物質量は3倍のままで、体積も3倍に増加して0.054L溶けることになります。因みに、対比を使用すると、
(✕)︰3.0✕10^5Pa︰0.018L=1.0✕10^5Pa︰xL
x=0.006Lになり間違いとなりますので、御注意下さい!
(1)水に溶解したCO2の質量〔g〕を求めよ。
(2)溶解したCO2を取り出せるものとして、圧力3.0✕10^5Paにすると、水に溶解したCO2の体積は何Lか。
(1)水に溶解したCO2の質量〔g〕を求めよ。
CO2が水1.0Lに溶ける量は、
1.72mL✕1000÷1000mL/L=1.72L
水200mLは、1.0Lの(2/10=1/5)だから、
1.72L✕(1/5)=0.344L
圧力1.0✕10^5Paの3倍の3.0✕10^5Paであることから、
(0.344L/22.4L/mol)✕44〔g/mol〕✕(3.0✕10^5Pa/1.0✕10^5Pa)≒2.027g 答.2.027g
(2)溶解したCO2を取り出せるものとして、圧力3.0✕10^5Paにすると、水に溶解したCO2の体積は何Lか。
体積は圧力に関係なく一定であるから、
答.0.344L
(1)0℃、1.0✕10^5Pa下での酸素は水3.0Lに何mol溶解するか答えよ。また、その質量〔g〕も求めよ。
(2)20℃、2.0✕10^5Pa下での酸素は水1.0Lに何mol溶解するか答えよ。また、その質量〔g〕も求めよ。
(3)20℃、4.0✕10^5Pa下での酸素が水1.0Lに溶解する体積〔L〕を求めよ。
(4)20℃、1.0✕10^5Paの空気を水100mLに接水させたとき、この水に溶解している酸素と窒素の質量を求めよ。ただし、20℃、1.0✕10^5Pa下での窒素の溶解度は0.015L、酸素と窒素の混合気体は体積百分率で、酸素60%、窒素40%とする。
(1)0℃、1.0✕10^5Pa下での酸素は水3.0Lに何mol溶解するか答えよ。また、その質量〔g〕も求めよ。
水に溶解する気体の物質量と質量は、気体の圧力と水の体積(❋ 水の量)に比例することから物質量は、
0.049L/(22.4L/mol)✕(3.0L/1.0L)=0.0065625mol 答.0.0066〔mol〕
質量は、
0.0066mol✕32〔g/mol〕=0.2112g 答.0.21〔g〕
(2)20℃、2.0✕10^5Pa下での酸素は水1.0Lに何mol溶解するか答えよ。また、その質量〔g〕も求めよ。
(1)と同じ考え方ですので物質量molは、
0.031L/(22.4L/mol)✕(2.0✕10^5Pa/1.0✕10^5Pa)=0.002767857〜mol 答.0.0028〔mol〕
質量gは、
0.0028mol✕32〔g/mol〕=0.0896g 答.0.090〔g〕
(3)20℃、4.0✕10^5Pa下での酸素が水1.0Lに溶解する体積〔L〕を求めよ。
1.0✕10^5Pa以上の圧力をどれだけかけても、温度一定では体積は圧力に関係なく一定(❋ 画像の気体の状態方程式により体積が増えることはない!)であることから、体積は0.031Lのままです! 答.0.031L
(4)20℃、1.0✕10^5Paの空気を水100mLに接水させたとき、この水に溶解している酸素と窒素の質量を求めよ。ただし、20℃、1.0✕10^5Pa下での窒素の溶解度は0.015L、酸素と窒素の混合気体は体積百分率で、酸素60%、窒素40%とする。
O2︰N2=60︰40=3︰2より、
O2の分圧︰(3/5)✕1.0✕10^5Pa
N2の分圧︰(2/5)✕1.0✕10^5Pa
100mLは、1Lの10分の1なので、(1.0L/10L)=0.1L、モル質量〔g/mol〕、分圧を乗じると、
O2の質量〔g〕︰0.031L/(22.4L/mol)✕(1/10)✕32〔g/mol〕✕(3/5✕1.0✕10^5Pa)/(1.0✕10^5Pa)=0.002657142〜g 答.0.0027〔g〕
N2の質量〔g〕︰0.015L/(22.4L/mol)✕(1/10)✕28〔g/mol〕✕(2/5✕1.0✕10^5Pa)/(1.0✕10^5Pa)=0.00075g 答.0.00075〔g〕
(1)0℃、5.0✕10^5Paの圧力を水5.0Lに対しかけたときの水素の質量〔g〕を求めよ。
(2)(1)の1.0✕10^5PaのもとでのH2の体積〔L〕を求めよ。
(1)0℃、5.0✕10^5Paの圧力を水5.0Lに対しかけたときの水素の質量〔g〕を求めよ。
9.4✕10^-4mol✕(5.0✕10^5Pa/1.0✕10^5Pa)✕(5.0L/1.0L)✕2〔g/mol〕=0.047g 答.0.047〔g〕
(2)(1)の1.0✕10^5PaのもとでのH2の体積〔L〕を求めよ。
物質量は圧力に比例するので5倍、体積(水の量)にも比例するので5倍すると、
9.4✕10^-4mol✕(5.0✕10^5Pa/1.0✕10^5Pa)✕(5.0L/1.0L)=0.0235mol≒2.4✕10^-2〔mol〕
気体の状態方程式にそれぞれの値を代入すると、
V〔L〕=(nRT)/P=(2.4✕10^-2〔mol〕✕8.31✕10^3〔Pa・L/K・mol〕✕273K)/(1.0✕10^5Pa)=0.5444712≒0.54 答.0.54〔L〕
N2の分圧︰1.0✕10^5Pa✕(2/5)=4.0✕10^4Pa
O2の分圧︰1.0✕10^5Pa✕(3/5)=6.0✕10^4Pa
全圧1.0✕10^5Paの内、N2とO2の分圧が、どの程度の割合を占めているかを、分母に1.0✕10^5Paを用いて計算しN2とO2の物質量molを求めます。
N2の物質量〔mol〕︰1.0✕10^-3mol✕(4.0✕10^4Pa/1.0✕10^5Pa)=4.0✕10^-4mol 答.4.0✕10^-4〔mol〕
O2の物質量〔mol〕︰2.2✕10^-3mol✕(6.0✕10^4Pa/1.0✕10^5Pa)=1.3✕10^-3mol 答.1.3✕10^-3〔mol〕
O2の分圧︰5.0✕10^5Pa✕(2/5)=2.0✕10^5Pa
N2の分圧︰5.0✕10^5Pa✕(3/5)=3.0✕10^5Pa
次に、全圧が0℃、5.0✕10^5Paであることに着目します。圧力をどれほど上げても体積は水1.0Lのときの体積から増加することはないので、体積に分圧を乗じるだけで体積〔L〕が求められます。
O2の体積︰4.9✕10^-2L✕(2.0✕10^5Pa/1.0✕10^5Pa)=0.098L 答.0.098L
N2の体積︰2.3✕10^-2L✕(3.0✕10^5Pa/1.0✕10^5Pa)=0.069L 答.0.069L
(1)0℃、3.0✕10^5Pa下の窒素は、水1.0Lに対して何L溶解するか。
(2)0℃、3.0✕10^5Pa下で、窒素は水3.0Lに何g溶解するか。
(3)20℃、4.0✕10^5Pa下で、窒素は水2.0Lに何g溶解するか。
(4)0℃、1.0✕10^5Pa下で酸素は0.049L溶解する。いま窒素と酸素の物質量比が1︰3の混合気体が0℃、2.0✕10^5Pa下で水1.0Lに接触しているとき、この水1.0Lに溶解する窒素と酸素の質量を、有効数字2桁まで求めよ。
(1)0℃、3.0✕10^5Pa下の窒素は、水1.0Lに対して何L溶解するか。
この問題で紛らわしいのが、「何L溶解するか?」です。これは言い換えた方が理解しやすいです。「何L溶解するか?=体積〔L〕を求めよ。」として考えると、圧力が3倍になると物質量も3倍溶けますが、体積は圧力に関係なく一定であり、1.0✕10^5Pa下での体積と同じ体積ですから、
答.0.023L
(2)0℃、3.0✕10^5Pa下で、窒素は水3.0Lに何g溶解するか。
まず、水に溶けている窒素の物質量を求めると、
0.023L/(22.4L/mol)≒0.0010mol
圧力3倍、水の体積3倍ですので、物質量にモル質量と一緒に乗じると、
0.023L/(22.4L/mol)✕28〔g/mol〕✕(3.0✕10^5Pa/1.0✕10^5Pa)✕(3.0L/1.0L)=0.25875g 答.0.26〔g〕
(3)20℃、4.0✕10^5Pa下で、窒素は水2.0Lに何g溶解するか。
まず、水に溶けている窒素の物質量を求めると、
0.015L/(22.4L/mol)≒0.00067mol
圧力4倍、水の体積2倍ですので、物質量にモル質量と一緒に乗じると、
0.015L/(22.4L/mol)✕28〔g/mol〕✕(4.0✕10^5Pa/1.0✕10^5Pa)✕(2.0L/1.0L)=0.15g 答.0.15〔g〕
(4)0℃、1.0✕10^5Pa下で酸素は0.049L溶解する。いま窒素と酸素の物質量比1︰3の混合気体が0℃、2.0✕10^5Pa下で水1.0Lに接触しているとき、この水1.0Lに溶解する窒素と酸素の質量を、有効数字2桁まで求めよ。
まずN2とO2の分圧を求めると、
N2の分圧︰2.0✕10^5Pa✕(1/4)=5.0✕10^4Pa
O2の分圧︰2.0✕10^5Pa✕(3/4)=1.5✕10^5Pa
N2とO2の物質量に分圧とモル質量を乗じると、
N2の質量︰0.023L/(22.4L/mol)✕(5.0✕10^4Pa/1.0✕10^5Pa)✕28〔g/mol〕=0.014375g 答.0.014〔g〕
O2の質量︰0.049L/(22.4L/mol)✕(1.5✕10^5Pa/1.0✕10^5Pa)✕32〔g/mol〕=0.105g 答.0.11〔g〕
今回は、ヘンリーの法則について問題文により理解して頂こうと、私なりの問題文を作成してみました。問題文をイメージすることで理解度も増したのではないでしょうか。
ヘンリーの法則に限らず、問題の解答を観ると案外、(たった、これだけの事か!)と思われる方も少なくないと思います。多くの問題をこなす事も大事ですが、やはり問題文をイメージしながら理解する事が重要なのではないでしょうか。
特に1つの問題に、分圧とは全く関係のない問題が出て来ると、分圧の問題なのか、そうでないのかで迷ってしまう事もあると思いますが、ゴチャ混ぜにならない様に、ここでも問題のイメージを重要視されたらハッキリと区別が付くのではないでしょうか。
さて、次回もヘンリーの法則に負けない様な記事に努めますので、よろしくお願い致します!
それでは、この辺で、 See you!




















